CNVs(copy number variations)是除了SNVs、INDELs之外另一种可能导致孟德尔遗传疾病的变异类型,指的是大片段(1kb到几个Mb)的碱基出现拷贝数的变异(del、dup等)。
目前常用的关于CNVs的数据库有DGV、DECIPHER等,以下链接可供参考。
- 健康人群 CNV: Genomic Variants www.projects.tcag.ca/variation
- 神经发育异常的患者 CNVs: DECIPHER www.sanger.ac.uk/PostGenomic/decipher/
- 染色体异常的患者 CNVs: www.ukcad.org.uk/cocoon/ukcad、www.isca.genetics.emory.edu/
- 染色体非平衡变异的患者 CNVs: www.ecaruca.net
目前临床上对于CNVs的检测一般有CMA、MLPA、CNV-se、aCGH等技术,但是对于WES、WGS的数据也可以使用软件进行call CNVs。
目前有很多进行call CNVs的软件,本文主要记录cnvnator的安装和使用。
cnvnator相关文章发表在2011年的《Genome research》上,而相关的软件也挂在了github上,网址如下:https://github.com/abyzovlab/CNVnator
cnvnator最大的一个缺点就是安装十分不便,和其他软件相比,这基本上是最被大家吐槽的一点,其次是运行所占内存也是较大的。
当然你可以选择现成的docker使用
1
$ docker pull diploid/cnvnator
我这里记录并分享一下我的使用经历包括安装经历。
首先是安装
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25# 笔者是作为管理员在Root的权限下安装的,可以在个人用户下安装
# 首先是root的安装,root可以理解为一个软件,也是cnvnator所依赖的
$ git clone https://github.com/root-project/root.git
$ mkdir build
$ cd build
$ cmake ../root
$ make -j 4
$ source bin/thisroot.sh
# 这里提醒一下,笔者安装过多次root,各种版本的,新的、旧的,无一都失败了,只有上述这个成功了
# 接下来就是CNVnator的安装,
$ git clone https://github.com/abyzovlab/CNVnator.git
$ cd CNVnator
# 此处的用你的samtools安装位置在CNVnator目录下建立软链接
$ ln -s /your/path/of/samtools-1.9/ samtools
# 安装依赖包yeppp
$ mkdir yeppp && cd yeppp
$ wget http://bitbucket.org/MDukhan/yeppp/downloads/yeppp-1.0.0.tar.bz2
$ tar xjf yeppp-1.0.0.tar.bz2
$ make clean
$ make LIBS="-lcrypto"
# 此处将root软件加入变量中
$ vim .bashrc
加入:export LD_LIBRARY_PATH=/your/path/of/root/build/lib:$LD_LIBRARY_PATH
$ source .bashrc
# 到这里就安装完了,你也可以建立一个软链接把cnvnator链接到bin目录下,这样就可以直接用cnvnator作为命令可以看到安装还是很麻烦的,笔者也是安装了N次才成功,都快崩溃的那种。
接下来是使用记录,使用还是很方便的,可以安装github的说明一步一步来,没有什么太难的地方,这里稍微记录一下并介绍个别参数。
以我自己的数据为例,我的是生殖细胞系的WGS数据,输入文件是已经比对完的bam文件。
1
2
3
4
5
6
7$ cnvnator -root sample.root -tree /your/path/of/bam
$ cnvnator -root sample.root -his 100 -d /your/path/of/hg19
$ cnvnator -root sample.root -stat 100
$ cnvnator -root sample.root -partition 100
$ cnvnator -root sample.root -call 100 > sample.cnvnator
$ awk '{ print $2 } END { print "exit" }' sample.cnvnator | cnvnator -root sample.root -genotype 100 > sample.gt
$ /your/path/of/CNVnator/cnvnator2VCF.pl -prefix sample -reference hg19 sample.cnvnator /your/path/of/hg19 > sample.vcf上面就是常规步骤了,介绍几个点:
首先是 -his 参数的值,也就是bin_size的值,这个可以根据CNVnator作者的建议,根据测序深度的不同进行调整:100X: 30;20-30X: 100;4-6X: 500;再低就1000
其次是 -d 参数,关于这个参数,官网有两种用法:
- 如果使用 -d 那就后面接参考基因组所在目录,作者自己是在 hg19 下有各个不同染色体的fasta文件,虽然按照说明是只要目录下有参考基因组就行了。这里笔者一开始目录中只有合并后的hg19的文件,发现下面的步骤报错,后来就重新下载hg19文件,解压后没有合并,运行正常。
- 如果使用 -fasta 参数就在后面跟参考基因组的压缩文件,笔者是把 hg19.fa 压缩成了 hg19.fa.gz ,但是后面还是报错了
第六句
awk那一句可以不运行,主要是看genotype,不影响最后一步转换为vcf文件
到这一步其实也就差不多了,那么下面是关于CNVs数据的一些简单处理方式和意见的记录,这一块笔者也没有仔细去研究,如果有需要可以单独交流。
关于CNV结果的注释,这里参考annovar注释:
1
2$ perl convert2annovar.pl -format vcf4old sample.vcf > sample.avinput
$ perl table_annovar.pl W001.avinput /your/path/of/annovar/humandb/ --buildver hg19 -remove -out sample -protocol refGene,cytoBand,omim201806,gwasCatalog,CCRS,phastConsElements100way,phastConsElements46way,phastConsElements46wayPlacental,phastConsElements46wayPrimates,tfbsConsSites,rmsk,dgvMerged,HIP,Constraint -operation g,r,r,r,r,r,r,r,r,r,r,r,r,r -nastring . --thread 12其实对于 CNVs 的注释和筛选,所能使用的数据库并不像 SNVs 那么多,所幸的是CNVs的结果也没那么多。
上面注释所涉及的数据库大多数能在annovar中直接下载,除了omim201806、CCRS、HIP、Constraint。
OMIM的数据可以在OMIM官网通过申请下载,这里不方便挂出来,不过笔者最近一次申请都过去几个月了,OMIM还是没有把链接发过来。
CCRS的数据可以在笔者之前的文章,关于注释的那一篇中下载并修改格式,但是用在CNVs中参考价值可能不大,可自行查阅。
HIP和Constraint的数据来源于DECIPHER,可以作为参考,下面记录一下如何下载并转换格式。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19# DECIPHER数据库提供了在线的可视化的检索方式,可以查看相关变异的很多信息,包括表型、致病性等,这些信息都是临床或科研单位上传的。其中DECIPHER可供下载的数据包括以下三种
# Haploinsufficiency Predictions:
# Updated predictions of haploinsufficiency as described by Huang et al. (2010, PLoS Genetics). Available as a Bed file for download from the link above.
$ wget https://decipher.sanger.ac.uk/files/downloads/HI_Predictions_Version3.bed.gz
# Population Copy-Number Variation Frequencies
# Common copy-number variants and their frequencies, as used and displayed in DECIPHER.
$ wget https://decipher.sanger.ac.uk/files/downloads/population_cnv.txt.gz
# Development Disorder Genotype – Phenotype Database (DDG2P)
# a curated list of genes reported to be associated with developmental disorders, compiled by clinicians as part of the DDD study to facilitate clinical feedback of likely causal variants. Please note: This file is maintained by the European Bioinformatics Institute. Its contents may differ from DECIPHER due to different update cycles.
$ wget http://www.ebi.ac.uk/gene2phenotype/downloads/DDG2P.csv.gz
# 上面是下载了三个数据库,当然下面只用到了两个,还有一个频率数据库笔者也不知道怎么去注释和使用比较好
# 上述三个数据库直接用gunzip去解压就行
# pLI:
$ awk -F "\t" '{print 0"\t"$3"\t"$5"\t"$6"\t"$20}' Constraint.txt > hg19_Constraint.txt
$ sed -i '1d' hg19_Constraint.txt
# HIP:
$ sed -i '1d' HI_Predictions_Version3.bed
$ bedtools sort -i HI_Predictions_Version3.bed > HIP.txt
$ awk -F "\t" '{print 0"\t"$1"\t"$2"\t"$3"\t"$4}' HIP.txt > hg19_HIP.txt除此之外,对于CNVs的研究也可以考虑从trio样本出发。考虑思路和snv类似,就是从遗传模式考虑,比如患者父母正常的情况下,可以寻找de novo、AR类型的变异。还有就是可以考虑将CNV的数据结合SNV/INDEL一起分析,主要就是CNV可能与SNV/INDEL构成复合杂合等情况。当然这些都是一些思路。
水平有限,要是存在什么错误请指出,可发送邮件至shiyuant@outlook.com!请大家多多批评指正,相互交流,共同成长,谢谢!!!
python: numpy学习笔记
列表与array的区别
- 在实现层面,数组基本上包含一个指向连续数据块的指针。另一方面,Python列表包含一个指向指针块的指针,这其中的每一个指针对应一个完整的Python对象。另外,列表的优势是灵活,因为每个列表元素是一个包含数据和类型信息的完整结构体,而且列表可以用任意类型的数据填充。固定类型的NumPy式数组缺乏这种灵活性,但是能更有效地存储和操作数据。
导入numpy
1 | import numpy as np |
array的创建
从列表创建数组
- 通过 list 创建一维 array
1 | list1 = [1,3,5,7] |
[1 3 5 7]
<class 'numpy.ndarray'>- 通过 list 创建二维 array
1 | list2 = [[1,2,4,8],[4,5,9,3]] |
[[1 2 4 8]
[4 5 9 3]]
<class 'numpy.ndarray'>- 如果需要明确数组的数据类型,可以用
dtype关键字
1 | np.array([1, 3, 4], dtype='float32') |
array([1., 3., 4.], dtype=float32)从头创建数组
- 通过范围创建 array
1 | # 线性序列 |
array([10, 9, 8, 7, 6, 5, 4, 3, 2])1 | # 创建五个元素的数组,这5个数均匀地分配到0-1 |
array([0. , 0.25, 0.5 , 0.75, 1. ])- 生成特殊矩阵
1 | # 全零矩阵 |
array([0, 0, 0, 0, 0])1 | # 全一矩阵 |
array([1., 1., 1., 1., 1.])1 | # 默认值一直的矩阵 |
array([[3.4, 3.4, 3.4, 3.4, 3.4],
[3.4, 3.4, 3.4, 3.4, 3.4],
[3.4, 3.4, 3.4, 3.4, 3.4]])1 | # 单位矩阵 |
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])1 | # 对角线矩阵 |
array([[1, 0, 0, 0],
[0, 2, 0, 0],
[0, 0, 3, 0],
[0, 0, 0, 4]])1 | # 创建一个由3个整型数组成的未初始化的数组 |
array([1., 1., 1.])- 生成随机数组
- random生成0到1之间的随机数
- uniform生成均匀分布随机数
- randn生成标准正态的随机数
- normal生成正态分布
- shuffle随机打乱顺序
- seed设置随机种子数
1 | # 设计随机种子 |
1 | # 创建一个3*3、在0-1均匀分布的随机数组成的数组 |
[[0.69646919 0.28613933 0.22685145]
[0.55131477 0.71946897 0.42310646]
[0.9807642 0.68482974 0.4809319 ]]1 | # 打乱随机数 |
[[0.9807642 0.68482974 0.4809319 ]
[0.69646919 0.28613933 0.22685145]
[0.55131477 0.71946897 0.42310646]]1 | # 创建一个3*3的、均值为0,方差为1的正态分布的随机数数组 |
array([[ 1.26593626, -0.8667404 , -0.67888615],
[-0.09470897, 1.49138963, -0.638902 ],
[-0.44398196, -0.43435128, 2.20593008]])1 | # 创建一个3*3,[0, 10)区间的随机整型数组 |
array([[8, 0, 7],
[9, 3, 4],
[6, 1, 5]])Numpy数据类型
指定方式
字符串
dtype='int16'numpy对象
dtype=np.int16数据类型
数据类型:描述
- bool_:布尔值(真、True 或假、False),用一个字节存储
- int_ : 默认整型(类似于 C 语言中的 long,通常情况下是 int64 或 int32)
- intc_ : 同 C 语言的 int 相同(通常是 int32 或 int64)
- intp : 用作索引的整型(和 C 语言的 ssize_t 相同,通常情况下是 int32 或 int64)
- int8 : 字节(byte,范围从–128 到 127)
- int16 : 整型(范围从–32768 到 32767)
- int32 : 整型(范围从–2147483648 到 2147483647)
- int64 : 整型(范围从–9223372036854775808 到 9223372036854775807)
- uint8 : 无符号整型(范围从 0 到 255)
- uint16 : 无符号整型(范围从 0 到 65535)
- uint32 : 无符号整型(范围从 0 到 4294967295)
- uint64 : 无符号整型(范围从 0 到 18446744073709551615)
- float_ : float64 的简化形式
- float16 : 半精度浮点型:符号比特位,5 比特位指数(exponent),10 比特位尾数(mantissa)
- float32 : 单精度浮点型:符号比特位,8 比特位指数,23 比特位尾数
- float64 : 双精度浮点型:符号比特位,11 比特位指数,52 比特位尾数
- complex_ : complex128 的简化形式
- complex64 : 复数,由两个 32 位浮点数表示
- complex128 : 复数,由两个 64 位浮点数表示
查看属性
1 | # shape |
(2, 4)1 | # size 元素的个数 |
81 | # 数据类型 |
dtype('int32')1 | # 数组的维度 |
21 | # 每个数组元素字节大小 |
41 | # 数组总字节大小 |
32数据的索引
获取单个元素
对于一维数组,直接通过中括号指定索引获取第i个值(从0开始计数)
1
x[1]
用负值索引末尾索引
1
x[-1]
多维数组中,可以用逗号分隔的索引元组获取元素
1
x[2, -1]
用以上索引方式修改元素值
1
x[0, 0] = 12
- NumPy 数组是固定类型的。这意味着当你试图将一个浮点值插入一个整型数组时,浮点值会被截短成整型。并且这种截短是自动完成的,不会给你提示或警告,所以需要特别注意这一点!
数据的切片
1 | x[start:stop:step] |
1 | import numpy as np |
array([0, 1, 2, 3, 4])1 | x[5:] # 索引5以后的元素 |
array([5, 6, 7, 8, 9])1 | x[4:7] # 索引4到6 |
array([4, 5, 6])1 | x[::2] # 隔一个元素 |
array([0, 2, 4, 6, 8])1 | x[::-1] # 逆序取所有元素 |
array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])1 | x[5::-2] # 从索引5隔一个逆序 |
array([5, 3, 1])多维子数组
1 | x2 = np.array([range(1 + i, 5 + i) for i in range(5)]) |
array([[1, 2, 3],
[2, 3, 4]])1 | x2[:, ::2] # 所有行,隔一列 |
array([[1, 3],
[2, 4],
[3, 5],
[4, 6],
[5, 7]])1 | x2[::-1, ::-1] # 逆序 |
array([[8, 7, 6, 5],
[7, 6, 5, 4],
[6, 5, 4, 3],
[5, 4, 3, 2],
[4, 3, 2, 1]])行、列获取
- 一个冒号(:)表示空切片
1 | x2[:, 1] # 第二列 |
array([2, 3, 4, 5, 6])1 | x2[1, :] # 第二行 |
array([2, 3, 4, 5])1 | x2[1] # 行的简便写法 |
array([2, 3, 4, 5])非副本视图的子数组
- 是数组切片返回的是数组数据的视图,而不是数值数据的副本
- 意思就是说,当修改子数组的数据时,原数据也会被修改
- 它意味着在处理非常大的数据集时,可以获取或处理这些数据集的片段,而不用复制底层的数据缓存
创建数组的副本
通过copy()来完成复制数组里的数据或者子数组
1 | x_sub = x2[:2, :2].copy() |
数据的变形
通过reshape()实现数组变形
1 | np.arange(1, 10).reshape((3, 3)) |
原始数组的大小和变形后数组的大小一致
如果不能保证上述条件,
-1表示自动填充位置的维度1
np.arange(1, 10).reshape((3, -1))
使用newaxis将一个一维数组转变为二维的行或列的矩阵
1
2
3
4# 行矩阵
x[np.newaxis, :]
# 列矩阵
x[:, np.newaxis]
数组的拼接和分裂
数组的拼接
np.concatenate- 以
数组元组或数组列表作为第一个参数
- 以
1 | # 拼接两个数组 |
array([1, 2, 3, 3, 2, 1])1 | # 拼接多个数组 |
array([ 1, 2, 3, 3, 2, 1, 11, 11, 11])1 | # 二维数组拼接 |
array([[1, 2, 3, 4],
[2, 3, 4, 5],
[3, 4, 5, 6],
[1, 2, 3, 4],
[2, 3, 4, 5],
[3, 4, 5, 6]])1 | # 按第二个轴拼接,左右拼接 |
array([[1, 2, 3, 4, 1, 2, 3, 4],
[2, 3, 4, 5, 2, 3, 4, 5],
[3, 4, 5, 6, 3, 4, 5, 6]])np.vstack垂直栈
1 | np.vstack([x, y]) |
array([[1, 2, 3],
[3, 2, 1]])np.hstack水平栈
1 | np.hstack([x, y]) |
array([1, 2, 3, 3, 2, 1])np.dstack沿着第三个维度拼接数组
1 | np.dstack([x, y]) |
array([[[1, 3],
[2, 2],
[3, 1]]])数组的分裂
- 与拼接相反的过程,通过
np.split、np.hsplit和np.vsplit来实现 - 传递一个索引列表作为参数,索引列表记录的是分裂点位置
- N个分裂点会得到 N + 1 个子数组
np.split
1 | x = [1, 2, 3, 4, 5, 6, 7] |
[array([1, 2, 3]), array([4, 5]), array([6, 7])]np.vsplit()
1 | grid = np.arange(16).reshape((4,-1)) |
[array([[0, 1, 2, 3],
[4, 5, 6, 7]]), array([[ 8, 9, 10, 11],
[12, 13, 14, 15]])]np.hsplit()
1 | np.hsplit(grid, [2]) |
[array([[ 0, 1],
[ 4, 5],
[ 8, 9],
[12, 13]]), array([[ 2, 3],
[ 6, 7],
[10, 11],
[14, 15]])]np.dsplit()
- 向量操作
- 通过简单地对数组执行操作来实现,这里对数组的操作将会被用于数组中的每一个元素
数组的运算
| 运算符 | 通用函数 | 描述 |
|---|---|---|
| + | np.add | 加法 |
| - | np.subtract | 减法 |
| - | np.negative | 负数 |
| * | np.multiply | 乘法 |
| / | np.divide | 除法 |
| // | np.floor_divide | 地板除/求整数 |
| ** | np.power | 指数运算 |
| % | np.mod | 模/余数 |
绝对值
1 | # 三角函数 |
theta = [0. 1.57079633 3.14159265]
sin(theta) = [0.0000000e+00 1.0000000e+00 1.2246468e-16]
cos(theta) = [ 1.000000e+00 6.123234e-17 -1.000000e+00]
tan(theta) = [ 0.00000000e+00 1.63312394e+16 -1.22464680e-16]1 | # 反三角函数 |
x = [-1, 0, 1]
arcsin(x) = [-1.57079633 0. 1.57079633]
arccos(x) = [3.14159265 1.57079633 0. ]
arctan(x) = [-0.78539816 0. 0.78539816]指数和对数
- 自然数的指数运算:np.exp
- 2的指数运算:np.exp2
- 自定义的指数运算:np.power
- 自然数为底的对数运算:np.log
- 2为底的对数运算:np.log2
- 10为底的对数运算:np.log10
- 以任意数为底的对数运算:np.log(m)/np.log(n)
- m 为底数
- n 为真数
1 | # 指数运算 |
x = [1, 2, 3, 4]
e^x = [ 2.71828183 7.3890561 20.08553692 54.59815003]
2^x = [ 2. 4. 8. 16.]
3^x = [ 3 9 27 81]1 | # 对数运算 |
ln(x) = [0. 0.69314718 1.09861229 1.38629436]
log2(x) = [0. 1. 1.5849625 2. ]
log10(x) = [0. 0.30103 0.47712125 0.60205999]1 | # 对于非常小的输入值的更好精度计算 |
exp(x) - 1 = [0. 0.0010005 0.01005017 0.10517092]
log(1 + x) = [0. 0.0009995 0.00995033 0.09531018]- logaddexp(a, b),在计算log(exp(a) + exp(b)) 更准确
高级的通用函数特性
指定输出
- 在进行大量运算时,有时候指定一个用于存放运算结果的数组是非常有用的。不同于创建临时数组,你可以用这个特性将计算结果直接写入到你期望的存储位置。所有的通用函数都可以通过 out 参数来指定计算结果的存放位置
1 | # 指定计算结果的存放位置 |
[ 0. 10. 20. 30. 40.]1 | # 写入指定数组的每隔一个元素的位置 |
[ 1. 0. 2. 0. 4. 0. 8. 0. 16. 0.]聚合
- reduce:望用一个特定的运算 reduce 一个数组,那么可以用任何通用函数的 reduce 方法。一个 reduce 方法会对给定的元素和操作重复执行,直至得到单个的结果
1 | x = np.arange(1, 6) |
15
120- accumulate: 存储每次计算的中间结果
1 | y = np.add.accumulate(x) |
[ 1 3 6 10 15]
[ 1 2 6 24 120]- 在一些特殊情况中,NumPy 提供了专用的函数(np.sum、np.prod、np.cumsum、np.cumprod ),它们也可以实现以上 reduce 的功能
外积
- 任何通用函数都可以用 outer 方法获得两个不同输入数组所有元素对的函数运算结果
1 | y = np.multiply.outer(x, x) |
[[ 1 2 3 4 5]
[ 2 4 6 8 10]
[ 3 6 9 12 15]
[ 4 8 12 16 20]
[ 5 10 15 20 25]]
[[ 2 3 4 5 6]
[ 3 4 5 6 7]
[ 4 5 6 7 8]
[ 5 6 7 8 9]
[ 6 7 8 9 10]]聚合:最大值、最小值和其他值
- 求和
- 通过np.sum实现
- array.sum()可便捷调用
- 最大值
- 通过np.min实现
- array.min()可便捷调用
- 最小值
- 通过np.max实现
- array.max()可便捷调用
1. 多维度聚合
通过指定axis用于沿着某个轴的方向进行聚合。
* axis = 0 表示每一列,即第一个轴被折叠
* axis = 1 表示每一行,即第二个轴被折叠1 | M = np.random.random((3,4)) |
[[0.36178866 0.22826323 0.29371405 0.63097612]
[0.09210494 0.43370117 0.43086276 0.4936851 ]
[0.42583029 0.31226122 0.42635131 0.89338916]]
5.022928013697376
[0.09210494 0.22826323 0.29371405 0.4936851 ]
[0.63097612 0.4936851 0.89338916]2. 其他聚合函数
- 大多数的聚合都有对 NaN 值的安全处理策略(NaN-safe),即计算时忽略所有的缺失值,这些缺失值即特殊的 IEEE 浮点型 NaN 值
| 函数名称 | NaN安全版本 | 描述 |
|---|---|---|
| np.sum | np.nansum | 计算元素的和 |
| np.prod | np.nanprod | 计算元素的积 |
| np.mean | np.nanmean | 计算元素的平均值 |
| np.std | np.nanstd | 计算元素的标准差 |
| np.var | np.nanvar | 计算元素的方差 |
| np.min | np.nanmin | 找出最小值 |
| np.max | np.nanmax | 找出最大值 |
| np.argmin | np.nanargmin | 找出最小值的索引 |
| np.argmax | np.nanargmax | 找出最大值的索引 |
| np.median | np.nanmedian | 计算元素的中位数 |
| np.percentile | np.nanpercentile | 计算基于元素排序的统计值 |
| np.any | N/A | 验证任何一个元素是否为真 |
| np.all | N/A | 验证所有元素是否为真 |
1 | heights = np.random.random(25) * 175 |
[165.22800319 87.82141828 109.19176656 20.23321914 55.52495932
72.59458709 151.60410263 43.82968894 84.53099625 172.47296248
90.90989587 107.25654201 21.11001655 144.60964009 105.53552247
95.38690113 59.98367091 53.22113808 72.97888693 119.22763401
153.20494731 89.32390906 117.12991202 102.5388967 109.35811287]
Mean height: 96.19229319557513
Standard deviation: 40.570450297029936
Minimum height: 20.233219138876752
Maximum height: 172.47296248187337
25th percentile: 72.59458709188556
Median: 95.38690113163136
75th percentile: 117.129912018397651 | %matplotlib inline |
广播
- 广播允许这些二进制操作用于不同大小的数组
1 | a = np.array([1, 2, 3]) |
array([6, 7, 8])- 可以认为这个操作是将数值5扩展或重复至数组
[5, 5, 5],然后执行加法 - 下面这个例子,一维数组为扩展或广播了,它沿着第二个维度扩展,扩展到匹配M数组的形状
1 | M = np.ones((3, 3)) |
array([[2., 3., 4.],
[2., 3., 4.],
[2., 3., 4.]])- 对两个数组同时广播,将 a 和b 都进行了扩展来匹配一个公共的形状,最终的结果是一个二维数组,例子如下:
1 | a = np.arange(3) |
[0 1 2]
[[0]
[1]
[2]]
array([[0, 1, 2],
[1, 2, 3],
[2, 3, 4]])广播的规则
- 如果两个数组的维度数不相同,那么小维度数组的形状将会在最左边补 1
- 如果两个数组的形状在任何一个维度上都不匹配,那么数组的形状会沿着维度为 1 的维度扩展以匹配另外一个数组的形状
- 如果两个数组的形状在任何一个维度上都不匹配并且没有任何一个维度等于 1,那么会引发异常
示例1
- 一个二维数组与一个一维数组相加:
M = np.ones((2, 3))
a = np.arange(3) - 形状如下
M.shape = (2, 3)
a.shape = (3,) - 可以看到,根据规则1,数组a的维度数更小,所以在其左边补1
M.shape -> (2, 3)
a.shape -> (1, 3) - 根据规则2,第一个维度不匹配,因此扩展这个维度以匹配数组
M.shape -> (2, 3)
a.shape -> (2, 3) - 现在两个数组的形状匹配了,可以看到它们的最终形状都为(2, 3)
1 | M = np.ones((2, 3)) |
array([[1., 2., 3.],
[1., 2., 3.]])示例2
- 两个数组都需要广播:
M = np.arange(3).reshape((3, 1))
a = np.arange(3) - 形状如下
M.shape = (3,1)
a.shape = (3,) - 可以看到,根据规则1,数组a的维度数更小,所以在其左边补1
M.shape -> (3, 1)
a.shape -> (1, 3) - 根据规则2,需要更新这两个数组的维度来相互匹配
M.shape -> (3, 3)
a.shape -> (3, 3) - 现在两个数组的形状匹配了,可以看到它们的最终形状都为(3, 3)
1 | M = np.arange(3).reshape((3, 1)) |
array([[0, 1, 2],
[1, 2, 3],
[2, 3, 4]])示例3
- 两个数组不兼容:
M = np.ones((3, 2))
a = np.arange(3) - 形状如下
M.shape = (3, 2)
a.shape = (3,) - 可以看到,根据规则1,数组a的维度数更小,所以在其左边补1
M.shape -> (3, 2)
a.shape -> (1, 3) - 根据规则2,第一个维度不匹配,因此扩展这个维度以匹配数组
M.shape -> (3, 2)
a.shape -> (3, 3) - 现在需要用到规则 3——最终的形状还是不匹配,因此这两个数组是不兼容的
1 | M = np.ones((3,2)) |
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-64-932af115d5e2> in <module>
1 M = np.ones((3,2))
2 a = np.arange(3)
----> 3 M + a
ValueError: operands could not be broadcast together with shapes (3,2) (3,) 广播的应用
数据的归一化
- 假设有一个有10个观察值的数组,每个观察值包含3个数值
X = np.random.random((10, 3))
- 计算每个特征的均值
Xmean = X.mean(0)
- 归一化操作
X_centered = X - Xmean
画一个二维数组
- 广播另外一个非常有用的地方在于,它能基于二维函数显示图像。我们希望定义一个函数 z = f (x, y),可以用广播沿着数值区间计算该函数
x = np.linspace(0, 5, 50)
y = np.linspace(0, 5, 50)[:, np.newaxis]
z = np.sin(x) ** 10 + np.cos(10 + y * x) * np.cos(x)
1 | x = np.linspace(0, 5, 50) |
<matplotlib.colorbar.Colorbar at 0x1409baa39b0>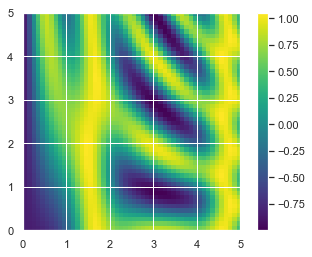
比较、掩码和布尔逻辑
比较操作
- 数组的逐元素操作,结果是一个布尔数据类型的数组
| 运算符 | 对应通用函数 | 描述 |
|---|---|---|
| == | np.equal | 等于 |
| != | np.not_equal | 不等于 |
| < | np.less | 小于 |
| <= | np.less_equal | 小于等于 |
> |
np.greater | 大于 |
>= |
np.greater_equal | 大于等于 |
1 | # 逐元素比较 |
[ True True False False False]
[False False False True True]
[ True True True False False]
[False False True True True]
[ True True False True True]
[False False True False False]
[False True False False False]操作布尔数组
统计记录的个数
np.count_nonzero(x < 6)
np.sum(x < 6) # False会被解释成0,True会被解释成1- sum的好处是,可以沿着行或列进行
- 快速检车任意或所有的这些值是否为True
np.any(x > 8)
np.all(x < 0)
- 上述两个函数也可以通过指定
axis来指定行列
1 | rng = np.random.RandomState(0) |
8
8
True
True- 布尔运算符
统计(0.5, 1)之间的数量和
np.sum((array > 0.5) & (inches < 1))
np.sum(~( (array <= 0.5) | (array >= 1) ))
| 运算符 | 通用函数 |
|---|---|
| & | np.bitwise_and |
| ^ | np.bitwise_xor |
| ~ | np.bitwise_not |
将布尔数组作为掩码
- 为了将特定值从数组中选出,可以进行简单的索引,即掩码操作
x[x < 5]
- 返回的是一个一维数组,它包含了所有满足条件的值。换句话说,所有的这些值是掩码数组对应位置为 True 的值。
1 | # 例子 |
Median precip on rainy days in 2014 (inches): 6.3526921480470175
Median precip on summer days in 2014 (inches): 4.619087615684484
Maximum precip on summer days in 2014 (inches): 9.930332610947918
Median precip on non-summer rainy days (inches): 6.533648713530407and 和 or 判断整个对象是真或假,而 & 和 | 是指每个对象中的比特位
- 使用 and 或 or 时,就等于让 Python 将这个对象当作整个布尔实体,所有非零的整数都会被当作是 True
bool(-1), bool(0)
(True, False)
bool(-1 and 0)
Flase
bool(-1 or 0)
True - 对整数使用 & 和 | 时,表达式操作的是元素的比特,将 and 或 or 应用于组成该数字的每个比特
bin(42)
‘0b101010’
bin(59)
‘0b111011’
bin(42 & 59)
‘0b101010’
bin(42 | 59)
‘0b111011’
- 使用 and 或 or 时,就等于让 Python 将这个对象当作整个布尔实体,所有非零的整数都会被当作是 True
NumPy 中有一个布尔数组时,该数组可以被当作是由比特字符组成的,其中 1 = True、0 = False。这样的数组可以用上面介绍的方式进行 & 和 | 的操作:
1 | A = np.array([1, 0, 1, 0, 1, 0], dtype=bool) |
array([ True, True, True, False, True, True])- 而用 or 来计算这两个数组时,Python 会计算整个数组对象的真或假,这会导致程序出错
- 同样,对给定数组进行逻辑运算时,你也应该使用 | 或 &,而不是 or 或 and
1 | x = np.arange(10) |
array([False, False, False, False, False, True, True, True, False,
False])花哨的索引
探索花哨的索引
- 概念,传递一个索引数组来一次性获得多个数组元素
1 | rand = np.random.RandomState(30) |
array([45, 53, 12])- 结果的形状与索引数组的形状一致,而不是与被索引的数组形状一致
1 | ind = np.array([[3, 7], [4, 5]]) |
array([[45, 53],
[12, 23]])- 对于多个维度的索引,和标准索引一样,第一个索引指的是行,第二个索引指的是列
1 | X = np.arange(12).reshape((3, 4)) |
array([ 2, 5, 11])- 索引值的配对遵循广播的规则
1 | X[row[:, np.newaxis], col] |
array([[ 2, 1, 3],
[ 6, 5, 7],
[10, 9, 11]])组合索引
- 花哨索引与其他索引方案结合使用
花哨索引和简单的索引组合使用
1 | X[2, [2, 0, 1]] |
array([10, 8, 9])花哨索引和切片组合
1 | X[1:, [2, 0, 1]] |
array([[ 6, 4, 5],
[10, 8, 9]])花哨索引和掩码组合使用
1 | mask = np.array([1, 0, 1, 0], dtype=bool) |
array([[ 0, 2],
[ 4, 6],
[ 8, 10]])示例:选择随机点
- 有一个 N×D 的矩阵,表示在 D 个维度的 N 个点
- 利用花哨的索引随机选取 20 个点——选择 20 个随机的、不重复的索引值,并利用这些索引值选取到原始数组对应的值
- 通常用于快速分割数据,即需要分割训练 / 测试数据集以验证统计模型时,以及在解答统计问题时的抽样方法中使用
1 | # 构建数组 |
(100, 2)1 | # 绘画 |
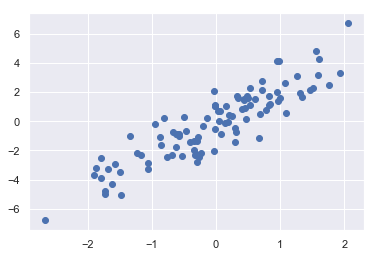
1 | #选取随机点 |
(20, 2)1 | # 画图 |
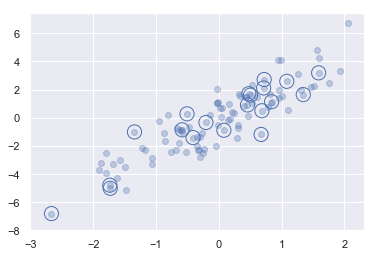
用花哨索引修改值
1 | x = np.arange(10) |
[ 0 99 99 3 99 5 6 7 99 9]1 | x[i] -= 10 |
[ 0 89 89 3 89 5 6 7 89 9]1 | # 不会累加 |
array([0., 0., 1., 1., 1., 0., 0., 0., 0., 0.])1 | # 累加 |
array([0., 0., 1., 2., 3., 0., 0., 0., 0., 0.])示例:数据区间划分
- 创建一个数组
1 | np.random.seed(42) |
[ 0.49671415 -0.1382643 0.64768854 1.52302986 -0.23415337 -0.23413696
1.57921282 0.76743473 -0.46947439 0.54256004 -0.46341769 -0.46572975
0.24196227 -1.91328024 -1.72491783 -0.56228753 -1.01283112 0.31424733
-0.90802408 -1.4123037 1.46564877 -0.2257763 0.0675282 -1.42474819
-0.54438272 0.11092259 -1.15099358 0.37569802 -0.60063869 -0.29169375
-0.60170661 1.85227818 -0.01349722 -1.05771093 0.82254491 -1.22084365
0.2088636 -1.95967012 -1.32818605 0.19686124 0.73846658 0.17136828
-0.11564828 -0.3011037 -1.47852199 -0.71984421 -0.46063877 1.05712223
0.34361829 -1.76304016 0.32408397 -0.38508228 -0.676922 0.61167629
1.03099952 0.93128012 -0.83921752 -0.30921238 0.33126343 0.97554513
-0.47917424 -0.18565898 -1.10633497 -1.19620662 0.81252582 1.35624003
-0.07201012 1.0035329 0.36163603 -0.64511975 0.36139561 1.53803657
-0.03582604 1.56464366 -2.6197451 0.8219025 0.08704707 -0.29900735
0.09176078 -1.98756891 -0.21967189 0.35711257 1.47789404 -0.51827022
-0.8084936 -0.50175704 0.91540212 0.32875111 -0.5297602 0.51326743
0.09707755 0.96864499 -0.70205309 -0.32766215 -0.39210815 -1.46351495
0.29612028 0.26105527 0.00511346 -0.23458713]- 手动计算直方图
1 | bins = np.linspace(-5, 5, 20) |
[-5. -4.47368421 -3.94736842 -3.42105263 -2.89473684 -2.36842105
-1.84210526 -1.31578947 -0.78947368 -0.26315789 0.26315789 0.78947368
1.31578947 1.84210526 2.36842105 2.89473684 3.42105263 3.94736842
4.47368421 5. ]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]- 为每个x找到合适的区间
1 | i = np.searchsorted(bins, x) |
[11 10 11 13 10 10 13 11 9 11 9 9 10 6 7 9 8 11 8 7 13 10 10 7
9 10 8 11 9 9 9 14 10 8 12 8 10 6 7 10 11 10 10 9 7 9 9 12
11 7 11 9 9 11 12 12 8 9 11 12 9 10 8 8 12 13 10 12 11 9 11 13
10 13 5 12 10 9 10 6 10 11 13 9 8 9 12 11 9 11 10 12 9 9 9 7
11 10 10 10]- 为每个区间加上1
1 | np.add.at(counts, i, 1) |
- 计数数组 counts 反映的是在每个区间中的点的个数,即直方图分布
- 画出结果
1 | plt.plot(bins, counts, linestyle='steps') |
[<matplotlib.lines.Line2D at 0x1409bbe1710>]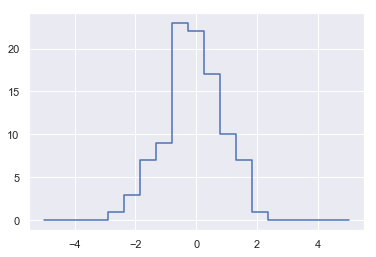
1 | # 上述结果的另一种实现方法 |
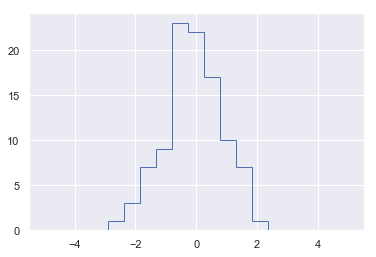
数组的排序
快速排序
- np.sort
不修改原始输入数组的基础上返回一个排好序的数组
- sort方法
用排序号的数组替代原始数组
- np.argsort
返回原始数据排好序的索引值
1 | x = np.array([3, 5, 2, 7, 8, 1]) |
array([1, 2, 3, 5, 7, 8])1 | x.sort() |
[1 2 3 5 7 8]1 | x = np.array([3, 5, 2, 7, 8, 1]) |
array([5, 2, 0, 1, 3, 4], dtype=int64)- 按行或列排序,使用axis参数
axis=0,按列排序
axis=1,按行排序
1 | rand = np.random.RandomState(42) |
[[6 3 7 4 6 9]
[2 6 7 4 3 7]
[7 2 5 4 1 7]
[5 1 4 0 9 5]]
[[2 1 4 0 1 5]
[5 2 5 4 3 7]
[6 3 7 4 6 7]
[7 6 7 4 9 9]]
[[3 4 6 6 7 9]
[2 3 4 6 7 7]
[1 2 4 5 7 7]
[0 1 4 5 5 9]]部分排序:分隔
- np.partition
输入数组和数字K
输出是一个新数组,左边是第K小的值,右边是任意排序的其他值。两个分隔的区域中,元素都是任意排序 - np.argpartition
计算分隔的索引值
1 | x = np.array([7, 3, 5, 9, 2, 1, 4, 8]) |
array([3, 1, 2, 4, 7, 5, 8, 9])1 | # 沿着多维数组的任意轴分隔 |
array([[3, 4, 6, 7, 6, 9],
[2, 3, 4, 7, 6, 7],
[1, 2, 4, 5, 7, 7],
[0, 1, 4, 5, 9, 5]])示例:K个最近邻
- 利用 argsort 函数沿着多个轴快速找到集合中每个点的最近邻
1 | # 在二维平面上创建一个有10个随机点的集合 |
<matplotlib.collections.PathCollection at 0x1409bc845c0>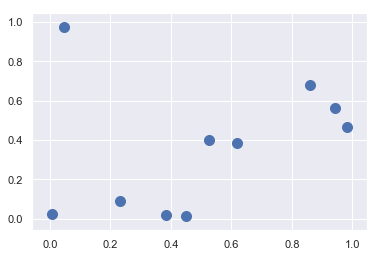
1 | # 计算两两数据点对间的距离 |
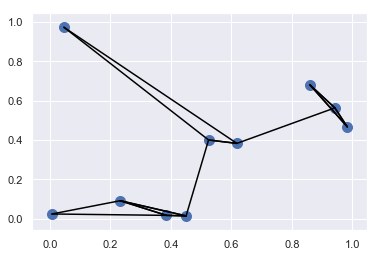
结构化数据
- 指定复合数据类型,构造一个结构化数组
1 | x = np.zeros(4, dtype=int) |
[('name', '<U10'), ('age', '<i4'), ('weight', '<f8')]1 | name = ['Alice', 'Bob', 'Cathy', 'Doug'] |
[('Alice', 25, 55. ) ('Bob', 45, 85.5) ('Cathy', 37, 68. )
('Doug', 19, 61.5)]1 | # 获取所有名字 |
array(['Alice', 'Bob', 'Cathy', 'Doug'], dtype='<U10')1 | # 获取数据第一行 |
('Alice', 25, 55.)1 | # 获取最后一行的名字 |
'Doug'1 | # 获取年龄小于30岁的人的名字 |
array(['Alice', 'Doug'], dtype='<U10')生成结构化数组
- 字典的方法
1 | np.dtype({'names':('name', 'age', 'weight'), |
dtype([('name', '<U10'), ('age', '<i4'), ('weight', '<f8')])1 | # 数值数据类型可以用 Python 类型或 NumPy 的 dtype 类型指定 |
dtype([('name', '<U10'), ('age', '<i4'), ('weight', '<f4')])1 | # 元组列表 |
dtype([('name', 'S10'), ('age', '<i4'), ('weight', '<f8')])1 | # 不指定类型的名称 |
dtype([('f0', 'S10'), ('f1', '<i4'), ('f2', '<f8')])简写的字符串格式
第一个(可选)字符是 < 或者 >,分别表示“低字节序”(little endian)和“高字节序”(bid endian),表示字节(bytes)类型的数据在内存中存放顺序的习惯用法
后一个字符指定的是数据的类型:字符、字节、整型、浮点型,等等
最后一个字符表示该对象的字节大小NumPy数据类型
NumPy数据类型符号 描述 示例 ‘b’ 字节型 np.dtype(‘b’) ‘i’ 有符号整型 np.dtype(‘i4’) == np.int32 ‘u’ 无符号整型 np.dtype(‘u1’) == np.uint8 ‘f’ 浮点型 np.dtype(‘f8’) == np.int64 ‘c’ 复数浮点型 np.dtype(‘c16’) == np.complex128 ‘S’、’a’ 字符串 np.dtype(‘S5’) ‘U’ Unicode 编码字符串 np.dtype(‘U’) == np.str_ ‘V’ 原生数据,raw data(空,void) np.dtype(‘V’) == np.void
跟高级的复合类型
- 创建一种类型,其中每个元素都包含一个数组或矩阵
1 | tp = np.dtype([('id', 'i8'), ('mat', 'f8', (3, 3))]) |
(0, [[0., 0., 0.], [0., 0., 0.], [0., 0., 0.]])
[[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]记录数组:结构化数组的扭转
- np.recarray
域可以像属性一样获取,而不是像字典的键那样获取
1 | # 消耗内存更多 |
array([25, 45, 37, 19])附:还有一些其他的
1 | #读取数据 |
[[0.417411 0.22210781 0.11986537 0.33761517 0.9429097 0.32320293
0.51879062]
[0.70301896 0.3636296 0.97178208 0.96244729 0.2517823 0.49724851
0.30087831]
[0.28484049 0.03688695 0.60956433 0.50267902 0.05147875 0.27864646
0.90826589]
[0.23956189 0.14489487 0.48945276 0.98565045 0.24205527 0.67213555
0.76161962]
[0.23763754 0.72821635 0.36778313 0.63230583 0.63352971 0.53577468
0.09028977]] [[0.417411 0.22210781 0.11986537 0.33761517 0.9429097 0.32320293
0.51879062]
[0.70301896 0.3636296 0.97178208 0.96244729 0.2517823 0.49724851
0.30087831]
[0.28484049 0.03688695 0.60956433 0.50267902 0.05147875 0.27864646
0.90826589]
[0.23956189 0.14489487 0.48945276 0.98565045 0.24205527 0.67213555
0.76161962]
[0.23763754 0.72821635 0.36778313 0.63230583 0.63352971 0.53577468
0.09028977]]1 | #截取数据 |
[0.90348221 0.39308051 0.62396996 0.6378774 0.88049907 0.29917202
0.70219827 0.90320616 0.88138193 0.4057498 ]
0.6378774010222266
[0.39308051 0.62396996 0.6378774 ]
[0.62396996 0.88049907 0.70219827 0.88138193]
[0.4057498 0.70219827 0.6378774 0.90348221]
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]
[15 16 17 18 19]
[20 21 22 23 24]]
[[6 7 8]]
[5 6 7 8]
[[ 5 6 7 8 9]
[15 16 17 18 19]]
[[ 1 2]
[ 6 7]
[11 12]
[16 17]
[21 22]]1 | #random.choice随机抽取 |
[[19. 6. 24. 22.]
[21. 17. 16. 2.]
[23. 15. 13. 11.]]
[[ 5. 14. 23. 15.]
[ 8. 24. 6. 18.]
[13. 10. 21. 11.]]
[[19. 21. 18. 11.]
[10. 21. 23. 19.]
[18. 19. 11. 20.]]1 | #矩阵操作 |
[[0 3 6]
[1 4 7]
[2 5 8]]
[[ 28 34]
[ 76 98]
[124 162]]
15
0.0
[[ 0.79111977 4.79625456 -2.59458683]
[ 0.72853989 -3.64821752 1.90992826]
[-2.01814852 -5.08596471 4.61137684]]1 | #数据的合并与展平 |
[1 2 3 4 5 6]
[1 2 3 4 5 6]1 | #多维数组的合并 |
[[0 1]
[2 3]
[0 1]
[2 3]]
[[0 1 0 1]
[2 3 2 3]]1 | #展平 |
[[0 1 2]
[3 4 5]]
[0 3 1 4 2 5]
[0 1 2 3 4 5]批量可视化fastp输出结果
- fastp是一个非常方便的基因组数据处理软件,之前在质控的环节就有用到它。
- 这个软件比较方便的地方就是对于处理前后的数据情况会输出一个可视化的网页报告,可以直接查看,报告内容也十分的简单易懂。
- 对于单个数据或者少数数据直接这么查看是比较方便的,但是对于大批量的数据进行处理以后,要还是一个一个报告查看,就让人很抓狂了。
- 最近就碰到了这么一个问题,于是写了一个python小脚本,进行批量结果的可视化,做一下笔记,怕以后忘了。
- 要进行批量可视化的前提是可视化的数据,fastp在处理完数据后,除了一个网页格式报告之外,还有一个json格式的报告,这就是我们的数据来源。
- 本脚本使用python3.x的版本,设计第三方库如下:
- pandas
- matplotlib
首先为这个脚本新建一个目录,并在目录下新建一个report目录(目录名随意)和一个python脚本(脚本名随意),report目录用来放fastp的json格式报告,如图,我的目录下面就放了两百多份报告。

- 这个实现本身很简单,主要要考虑的一点是WGS数据很多时候不是一个sample一对fastq文件,很多时候一个sample对应好多对fastq文件,那么fastp也会输出多个报告,对于这些报告我们要进行合并。
- 下面就来解析一下脚本
先上完整脚本
1 | import json, os |
首先导入相应的库,其中json和os是内置库,分别用来解析json文件以及查看文件。json格式的解析很简单,其实json可以看成是python里面的字典,下面是简单的json库使用:
1
2
3
4
5
6
7
8import json
# 输出 json 数据
with open('data.json', 'w') as f:
json.dump(data, f)
# 读取数据
with open('data.json', 'r') as f:
data = json.load(f)
一般情况下,在当前目录运行的脚本,直接用相对路径就行,但是也有可能你的报告不在当前目录下,那么第5行和第10行的
'./report'就要改成你报告所在目录的位置,同时report这个目录名也要改成你自己存放json格式的目录名。如何合并一个sample的报告结果
1
2
3for k,v in result_dict.items():
key = k.split('_')[0]
...这一步的工作就是合并结果,在我的结果里,虽然一个sample有时候会被分为好多个数据,但是数据的前缀的一部分都是一样的,且以
_分割。这个脚本提取了raw data中
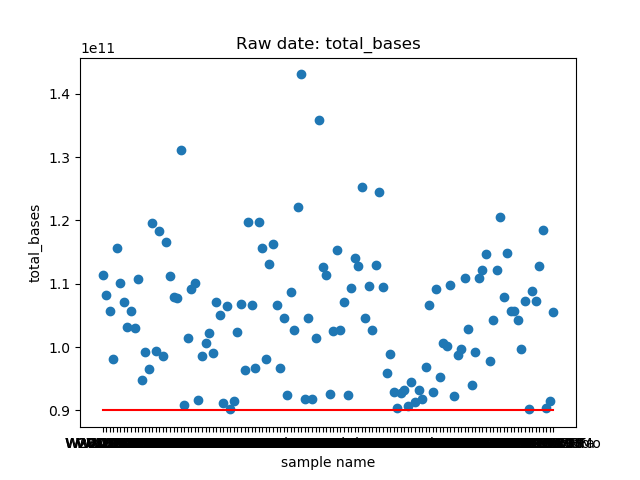
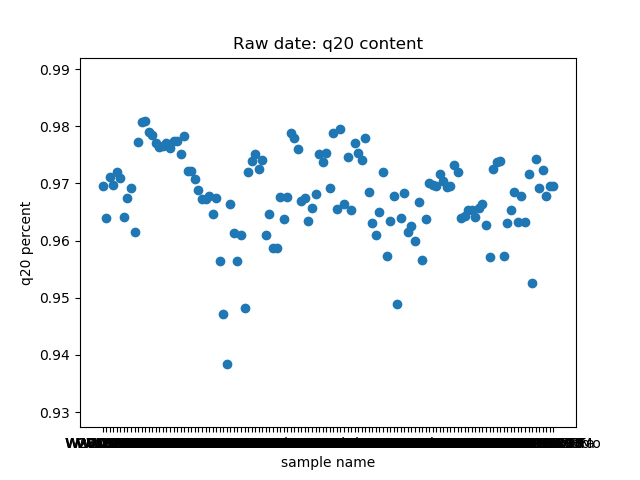
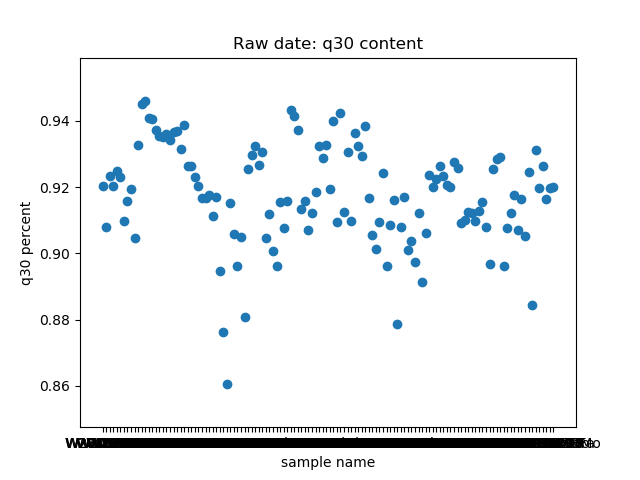
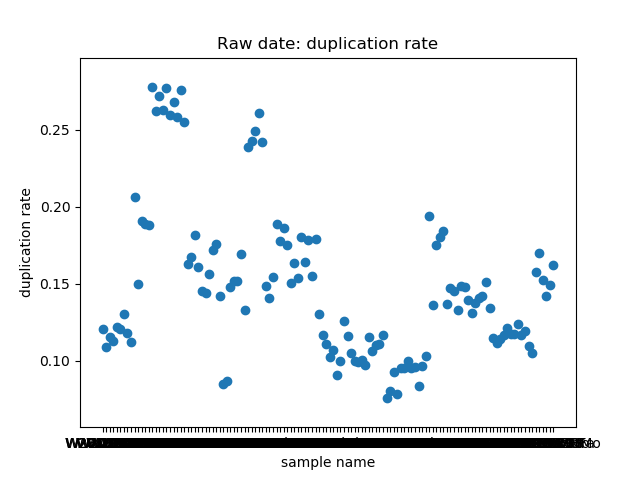
total_bases和q30_bases的数据,这是因为这一块是需要和测序公司核对的部分,一般公司需要交付 90G 的raw data,且Q30要80%以上。其实fastp结果里还有很多其他可以提取的数据,完全可以根据需要提取作图,还是很简单的。最后一个图是看一下,如果去掉duplicate的数据,那么raw data还有多少数据量。
展示一个结果图。
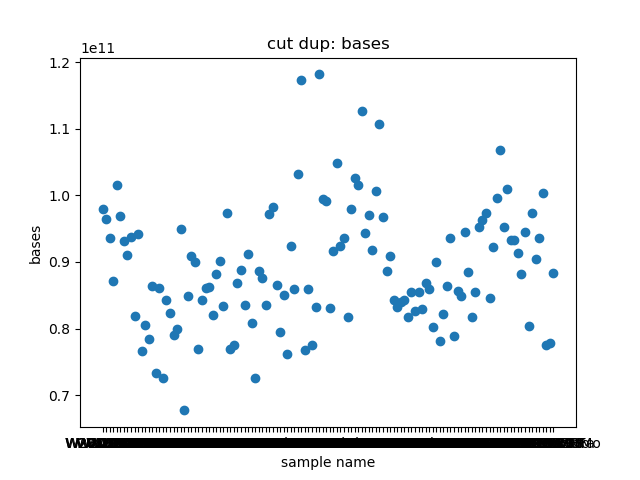
脚本本身超级简单,我看半天实在也不知道还有哪里需要解释的,如果有什么错误或者写的不好的还请见谅了。
水平有限,要是存在什么错误请指出,可发送邮箱至shiyuant@outlook.com!请大家多多批评指正,相互交流,共同成长,谢谢!!!
ACMG指南解读笔记(1)- PVS1
白纸黑字,还有中文版,其实也没啥好看不懂的,读懂它理解它并没有那么难,而我想的是怎么去实现它,限于本人专业水平有限,若有错误还请包容。
解读的多数内容基于ANNOVAR的注释!!!
- 原文不贴了,大体的意思我理解的就是,这个突变导致基因功能完全被破坏,那么就定义为PVS1(pathogenic very strong ,这里的数字不代表等级,只是表示序号,以示区分),同时指南也提了几个注意的点。
- 既然想要脚本实现,那么比较直观的方法就是流程图了,下面直接贴出这个证据实现的流程图:
- PVS1/pvs1.jpg)
这是基于InterVar源码理出来的逻辑图
来理解一下:
- frameshift,stopgain包含了指南中的无义突变、移码突变,说明一下,源码中还有‘nonsense’,但是该词条在ANNOVAR注释结果中是没有的(InterVar的筛选是基于ANNOVAR的),‘stopgain’可认为是‘nonsense’;同时“起始密码子变异”这一类变异在ANNOVAR中也是没有的,起始密码子在真核生物中可以认为只有AUG一种,如果发生变异了,只有一种情况,就是无法转录了,这种情况2/3能被检测出来并标为”exonic,splicing”,毕竟起始密码子就在RNA剪切位点上;“单个或多个外显子缺失”可以包含在上一种情况里;还有一个问题就是论文中作者提到了stop_less,但是在源码中似乎没有体现。
- 第二点就是要判断这些变异会不会导致功能丧失,这一点直接判断是很不好判断的,InterVar的做法是对ClinVar数据进行处理,挑出存在于MedGen数据库中的相关变异,过滤掉高频变异(频率大于5%)以及一些结果矛盾的变异。最后挑出的基因列表里,每个gene中至少有一个变异在Clinvar中为“pathogenic”,并与ExAC对LOF容忍度打分很低的基因取了并集,最后得到了这么一个list(挂在github上了)。
- 第三点,如果是在经典的剪接位点发生突变,这一点判断方法,主要是基于dbscSNV的打分来判断的,阈值是0.6,数据库在ANNOVAR上直接可以下载。
- 同时指南有几个附加注意点:
- 第一点我的解读就是判断某些突变的特异性,比如只有杂合错义突变时才致病, 而杂合无功能变异却是良性的,这个例子本身就是很特殊的,如果真碰到这个情况,且这种情况已知,那么一开始就可以特异性找出来或筛掉相关变异,如果一开始不知道,这一步也只是让某些变异有害性增强,在复查的时候也可以筛掉,所以影响不大。
- 第二点主要体现在对于exon的选取,作者筛掉了在第一和最后一个exon上的变异,并在下一步过滤了倒数第一个exon(InterVar提供了相关列表,挂在github上了)上靠近3‘端50bp的变异,这里不太明白的是为什么要筛掉第一个exon上的变异,指南中似乎没有提到相关的要求,而InterVar论文中也没有相关说明;同样的指南有提到倒数第二个exon,这里也没有体现。
- 第三点的一部分通过dbscSNV体现,其余的无法比较好的直接判断,所以没有体现,第四点,第五点同理,不好判断。
- 第一点我的解读就是判断某些突变的特异性,比如只有杂合错义突变时才致病, 而杂合无功能变异却是良性的,这个例子本身就是很特殊的,如果真碰到这个情况,且这种情况已知,那么一开始就可以特异性找出来或筛掉相关变异,如果一开始不知道,这一步也只是让某些变异有害性增强,在复查的时候也可以筛掉,所以影响不大。
- frameshift,stopgain包含了指南中的无义突变、移码突变,说明一下,源码中还有‘nonsense’,但是该词条在ANNOVAR注释结果中是没有的(InterVar的筛选是基于ANNOVAR的),‘stopgain’可认为是‘nonsense’;同时“起始密码子变异”这一类变异在ANNOVAR中也是没有的,起始密码子在真核生物中可以认为只有AUG一种,如果发生变异了,只有一种情况,就是无法转录了,这种情况2/3能被检测出来并标为”exonic,splicing”,毕竟起始密码子就在RNA剪切位点上;“单个或多个外显子缺失”可以包含在上一种情况里;还有一个问题就是论文中作者提到了stop_less,但是在源码中似乎没有体现。
从上面的分析可以得到,对于ACMG指南,解读和判断经常是很难面面俱到的,有些时候只能尽量通过一些方法来辅助判断,但是在使用这些辅助手段的时候就要慎重,辅助手段本身是存在一定的偏差的。
总结一下我的问题和我觉得可以改进的地方:
- 起始密码子第三个碱基发生突变的时候,这种情况InterVar是如何考虑的,不知道是我没看明白还是InterVar没有考虑到,如果是后者,那么就可以针对改进了(即使这种情况可能性可能很低)。
- stop_less这种变异是不是可能会造成功能丧失,作者论文中提到了,从我的逻辑来说应该是不太可能会的。
- 功能缺失基因列表如果能采用Clinvar结合HGMD,那么应该能更准确一点,这一点有条件的小伙伴完全可以考虑一下,更新list的。
- 不太明白为什么要过滤掉第一个exon上的变异,以及为什么没有过滤掉倒数第二个exon上的靠近3‘端50bp的变异。
- 起始密码子第三个碱基发生突变的时候,这种情况InterVar是如何考虑的,不知道是我没看明白还是InterVar没有考虑到,如果是后者,那么就可以针对改进了(即使这种情况可能性可能很低)。
以上问题非常欢迎各位交流指导!!!
水平有限,要是存在什么错误请指出,可发送邮件至shiyuant@outlook.com!请大家多多批评指正,相互交流,共同成长,谢谢!!!
ACMG指南解读笔记(0)- 定个小目标
好久没有更新内容,照理来说对于call出来的SNVs/INDELs,下一步的工作就是筛选了,一般的筛选方式大体会有这些步骤:
保留数据库中已报道的致病位点(Clinvar、HGMD)
过库筛选(人群频率数据库)
保留coding区域(一般是exonic和splicing,下同)
保留有害位点(通过预测软件打分)
去除非高度保守区同义突变(GERP++等判别)
遗传模式过滤
以及其他
如果在某疾病患者中(指单基因遗传病,符合孟德尔遗传定律,下同),找到了该疾病已经报道的致病突变位点,那大体来说,这个位点就会被判断为该患者的致病突变。
在这里,我们一般更认可HGMD中收录的记录,相对来说,Clinvar就是一个比较“脏”的数据库,因为这个公共数据库中的位点信息是大家都可以上传的,没有经过专门的筛选和“清洗”,真实性相对较差。而反过来,Clinvar是一个免费数据库,可以随时下载使用;HGMD的专业版收费是真的高,一般的课题组怕是很难吃得消,HGMD的公开版不收录近三年的信息(别看三年,差异很大,尤其是现在科学进展越来越快),只提供检索,不提供下载。所以要是买不起HGMD,Clinvar也就将就一点凑活用吧。
但是,经过上面的筛选,其实大多数病例的致病原因都是无法解释的。那么就需要我们常规的一些筛选策略了。其中首选的就是基于人群频率数据库的过滤。我们一般认为,一个变异在多数人身上存在,那这个变异应该是良性的(benign),看文献,绝大多数的方法里都有这一步。
Annovar提供了很多的人群频率数据库,那么我们怎么选呢?
- 考虑到种族特异性,尽量选择东亚人群数据库(1000gEAS等)
- 尽量选择多个数据库(1000g,ESP6500等)
- 尽量选择正常人群数据库
- 考虑选择大家常用的知名数据库(1000g,gnomad,ESP6500等)
- 考虑到种族特异性,尽量选择东亚人群数据库(1000gEAS等)
阈值的话可以考虑5%(常见变异和稀有变异的交界),1%(很多文献都是这个值),0.5%(稀有突变和罕见突变的交界),你要说区别有多大,得看你疾病的发病率了,我们做罕见疾病,筛选到后来,基本剩下的位点的人群频率都比上面三个数小,所以区别不大。但这一步能帮你筛掉很多的变异。
保留coding是因为noncoding的变异没有很好的筛选策略,而80%的遗传病病因可以用coding区突变来解释(教科书上这么说的),所以现在做WES的很多。
通过预测软件对位点的有害性进行打分。SIFT,Polyphen,MutationTaster,CADD是我们常用的四个软件,一般说半数以上预测有害,就认为有害。当然,既然是预测软件,就存在一定的偏差,可能会漏掉一些不常规的有害变异,或者保留一些良性变异。
同义突变不改变氨基酸,但目前的研究发现,并不是说同义突变就不致病,但是对于大多数同义突变,尤其是非保守区的同义突变,我们还是认为它是良性的。
遗传模式是基于家系数据进行判断致病性的一个比较好的方式。比如,当该疾病只在患者身上有临床表现,我们就考虑纯合突变,新发突变或复合杂合突变。
同时也会着重考虑OMIM上该疾病已经报道的相关基因上的变异位点。
还有一些其他的我也没考虑到的过滤方式(欢迎大家发邮件交流补充!!!)
- 可能有一些朋友要问,我为什么要根据上面的条件过滤?依据又是什么??还有什么值得注意的地方???有没有什么金标准????
- 说到金标准,还真是有的。
- 2015年的时候,由美国医学遗传学与基因组学学会(The American College of Medical Genetics and Genomics, ACMG),分子病理协会(the Association for Molecular Pathology, AMP)和美国病理学家协会(the College of American
Pathologists, CAP)的代表撰写修订了序列变异解读的标准和指南,发表在nature子刊GIM上,指南原文在这里能看到,当然也可以去GIM上搜。 - 对于遗传专业术语不太了解的同学,可能在解读原版指南的时候很痛苦。那也不用怕,在该指南发布后,国内外超过30家单位的几十位业界大佬共同翻译了该指南,链接在这里,这样至少在解读上轻松了一半。
- 在解读完该指南后,你就会发现,上述筛选条件,基本都有指南的影子。毕竟该指南是号称可直接应用于临床,所以理解该指南对于变异的筛选还是很有帮助的。
- 但问题也是有的,以下所列都是个人观点,若是理解不当望指出:
- 临床是临床,科研是科研,临床和科研的目的是不一样的,如果全用这套指南去科研,怕是很难找出新的位点或基因。
- 该指南甚是全面了,但是很多证据的解读,不同的人怕是存在分歧的。
- 该指南在理解上可能不是很难,但实际去判断就存在很大的困难了。
- 2017年的时候annovar的作者王凯大神根据指南写了一个软件InterVar,发表在AJHG上,原文链接在这里,软件挂在github上,链接在这里,网页版软件的链接在这里,结果文件intervar_20180118在annovar上直接可以下载,方法可参考我之前的文章。只能说大神不愧是大神,真是一件喜大普奔的事情。但是存在一些问题:
- 由于版权问题,作者用到的结果是基于Clinvar而不是HGDM
- 由于不同的疾病本身存在的特异性,加之指南有些证据难以通过软件进行判断,intervar一些证据是默认为False的,需要手动判断
- 网页版intervar虽然能手动较为直观的设定特异性参数,但是不利于批量判断,且不含indel信息
- 由于版权问题,作者用到的结果是基于Clinvar而不是HGDM
- 临床是临床,科研是科研,临床和科研的目的是不一样的,如果全用这套指南去科研,怕是很难找出新的位点或基因。
- 本着加深学习的目的,我决定逐条解读这些证据(共28个证据,16个角度)。本来想自己一个人这么做的,发现难度不小,有些证据我真的很难正确的解读,想组队讨论,又找不到又闲又感兴趣的(身边做这个的人太少啦,所以特别希望能有人一起交流讨论)。所以就打算写成系列文章挂出来,接受广大人民群众的diss。
- 我会基于中文版ACMG指南,参考InterVar文章和源码,较为详细的解读每一个证据(flag是立下来了,督促自己!),然后尽量重构Intervar。最后参考Sherloc: a comprehensive refinement of the ACMG–AMP variant classification criteria(基于指南的分析框架,让指南更便于实现)进行调整。
水平有限,要是存在什么错误请指出,可发送邮件至shiyuant@outlook.com!请大家多多批评指正,相互交流,共同成长,谢谢!!!
fastqc的线程与速度测试
之前文章写了bowtie2和bwa的比较,发完之后立刻被师姐批评指正了,然后师姐又给我补充了一个知识,就是不同软件都有它的最佳线程数,不是线程越高就跑的越快,直接一个软件定个24线程是不合理的。至于这个最佳线程数是多少,说明书要是没有的话,要么自己评测,要么问问作者。
我看了bwa的说明书,没有相关说明,粗略的查了一下帖子也没看到。让我自己评测一下bwa的速度,我是嫌麻烦的,于是我就尝试着评测一下fastqc。因为一开始我就是加大了这个的使用线程,也没考虑是不是有必要,而且这个速度也快,操作也方便,所以做个简单的速度测试。
软件是fastqc,选用的对象是一个cleaned data,还是比较大的,测试脚本如下:
1 | $ time fastqc -o singleout1/ -t 1 1.fq.gz |
结果如下:
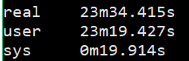
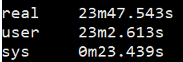
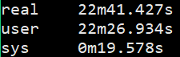
看到这个结果,我……有点吃惊的,居然都是一样的。那我脚本里写那么大的线程意义何在?
所以我又加了一个测试,测试多个样本下的不同线程的速度,当前文件夹下有4个fq文件。测试脚本如下:
1 | $ time fastqc -o allout1/ -t 1 *.fq.gz |
结果如下: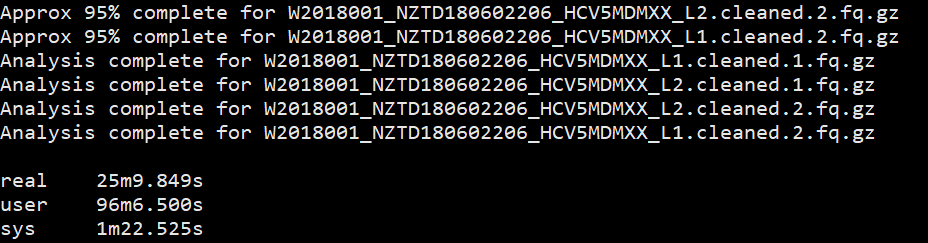

我想大家已经看出来了,对于单个样本,fastqc每增加一个线程并不改变运行速度,但是对于多个输入文件,每增加一个线程会多并行跑一个输入文件,就是说,比如输入四个文件,四线程会同时跑四个文件,单线程只能一个一个跑。
能得到一个结论还是挺开心的,那么以后在fastqc线程选择的时候也就知道多少的线程数是有必要的。
水平有限,要是存在什么错误请指出,可发送邮箱至shiyuant@outlook.com!请大家多多批评指正,相互交流,共同成长,谢谢!!!
WGS分析笔记(5)- annotation
在找到很多变异以后(本文具体指的是snv以及indel),我们需要做的就是进行注释了,这是因为无论WGS还是WES,都会call出大量的变异。即使是一个正常人,也会有百万数量级的变异(详见上一章),而我们需要做的是把其中可能有害的变异找出来。因此对于这么多的变异,就需要通过注释信息来筛选了(不同于call snv/indel以后的筛选,那是依据变异本身的可信度进行筛选的)。
对于不同的研究目的,目前用的注释软件还是不少的,有专门针对肿瘤数据的注释软件(如oncotator等),也有孟德尔遗传疾病测序数据常用的annovar、vep等。
本文主要讲的是通过annovar,对vcf文件进行注释,个人觉得annovar特别好用简单,说明书也写得很好,即使是我这种看了英语头晕的人,也能看的比较明白。
比较一下annovar和vep,annovar软件是需要先申请再下载的,对于研究机构是免费的,对商业机构是收费的,只要你拿学邮去申请,应该就没有问题。而vep是免费的,但是呢,安装起来超级麻烦,本文虽然不用vep,但会在后面附上我当初安装vep的笔记。
annovar很人性化的一点是,当你下载到软件以后,直接解压就能用了,不用安装。而你需要注释什么数据库,按照官网说明书的词条直接下载就行。
本文主要讲述我在做课题的时候是如何使用的,具体的细节可以参考官网说明书或者别的大神们的使用笔记。
首先是下载数据,annovar提供了大量的数据库,可以单独下载也可以批量下载,主要是来源于annovar自己网站以及ucsc的,你要是批量下载是完全没有必要的,因为一个数据库可能有很多的版本,也有很多数据库是你不需要的,还有一些数据库所占空间那是相当的大。举几个我常用的数据库为例(我只是举例一些,建议是看看说明书根据需要下载)。
1 | #注释基因 |
然后是输入格式的转换,对于注释所需的输入文件,只需要前五列按照avinput的要求就行了,格式如下。
1 | #分别以tab分隔 |
在注释完以后是不会保留原有的五列以外的内容的,转换脚本如下:
1 | $ perl convert2annovar.pl -format vcf4old in.vcf > out.avinput |
上面这个脚本除了把vcf转换为avinput以外,还会把一些多等位位点转换为单等位位点来注释,而格式之所以选用vcf4old,是因为我的输入格式是家系merge的vcf,一个vcf文件里有一家人的信息,如果是单个样本的话,直接用vcf4就行了。
用这种方式得到的结果就像我说的,注释完以后就没有保留 genotype等信息,除了前五列就只剩注释信息了。当然,也可以不转换格式,直接用vcf作为输入格式了,那么注释结果以标签的方式插入vcf文件之中,但是这样的话,会导致输出结果异常的占空间,因为,每一个数据库的头文件会反复出现在每一行被注释的变异中。提供参考脚本如下:
1 | # 输入是vcf文件,要加上参数-vcfinput |
虽然提供了这种方法,但我却是不建议的,尤其是我以WGS的文件作为输入,会使输出文件占很大的空间,但我又想保留 genotype信息,因为后面我需要这个信息判断变异的显隐性,这对于筛选是很关键的,那怎么办呢?
我想到的办法就是,在转换格式的时候,添加参数-includeinfo和-comment,前者的作用保留了genotype信息,后者保留了vcf的头文件。
1 | $ perl convert2annovar.pl -format vcf4old in.vcf -outfile out.avinput -comment -includeinfo |
转换完格式就是注释了,虽然annovar提供了多种注释方式,但是我们一般都是批量注释,即像上面那个注释的例子一样,下面来简单说一下怎么批量注释。
1 | $ table_annovar.pl out.avinput /your/path/of/humandb/ \ |
来详细说一下我这个脚本有什么需要注意的地方,而我又是怎么应用于实际课题中的。
首先是out.avinput,就是上面转换之后的输出文件;之后跟着的就是我们下载数据库的目录;我用的是hg19的参考基因组;-out是输出文件的路径和输出文件的前缀;-remove表示删除注释过程中的临时文件;-protocol表示注释使用的数据库,用逗号隔开;-operation 表示对应顺序的数据库的类型(g代表gene-based、r代表region-based、f代表filter-based,可对照说明书),用逗号隔开,与-protocol顺序一一对应;-nastring 表示用点号替代缺省的值。
annovar其实提供了好多个gene-based数据库下载,refGene是NCBI提供的,还有ensembl、UCSC提供的ensGene、knowGene,这三个数据库是有所差别的,至于怎么选择,建议就和使用的参考基因组来源一致即可,比如我用的是NCBI上下载的参考基因组,那么就用refGene。
-csvout 表示最后输出.csv文件,使用这个参数得到的是csv格式的文件,可以直接用excel打开,但是我没有使用,输出是tab分隔的txt文件,方便后续我写脚本处理。为什么“,”分隔的csv文件不适合处理呢?那是因为refgene的注释结果也是逗号分隔的,在分析的时候就会出现问题。
--thread是线程数,当然线程数越高注释速度越快。
到了这一步以后,其实结果还是前五列avinput的内容,后面是注释的内容,genotype的信息还是没有掉了,这个时候就加一步,来解决一下这个问题。
1 | $ grep -v "##" out.avinput | cut -f1-9 --complement > gt.txt |
很简单的两行命令,第一行提取了avinput文件里的genotype信息,然后第二行merge这个信息到注释完的文件上。这样得到的结果呢,又有注释信息,又有genotype信息,就很方便进行trio分析。
到这里其实就差不多了,可以进行下一步的筛选了,但是实际情况中,我们用到的数据库可能不止annovar提供的这些。毕竟annovar提供的数据库都是公开的数据库,而且对于日新月异的预测数据库等,annovar作者也不能做到每一种都去收录,如果你有一些自己下载的数据库,你该怎么利用annovar去注释呢?
这一类的数据库很多,比如omim需要申请才能下载,HGMD专业版需要付费订阅,这些annovar都是没有提供的。但是这些数据库在孟德尔遗传疾病中是很具有参考价值的,由于这两个都不能直接下载获得,这里也不详述,以两个近期发表在Nature Genetic上的公开的预测数据库为例,简述一下简单的方法构建自己的数据库。
annovar注释变异有两种注释方式,一个是基于区域,一个是基于位点,CCRS就是一个基于区域的有害性预测打分工具,其数据可在这里下载,分为常染色体和X染色体;S-CAP就是一个基于位点的splicing 区域有害性预测工具,其数据可以在这里下载。
CCRS
由于是基于区域的,那么在-operation参数里面呢是r,然后呢从网上下载下来的是一个bed文件,截取前十行,长这样。
- annotation/1.png)
这些信息其实我们只需要ccr_pct这一列的打分,为了方便起见,完全可以只保留前四列的内容,不然注释完会把所有前三列以后的内容都加到注释结果文件里。
那么这么一个文件是不能直接拿来用的,第一步就是改名。下载过annovar提供的数据库后可以知道,annovar使用的数据库都有自己的命名方式,这里的话直接改成 hg19_ccrs.txt即可,hg19表示所使用的参考基因组版本,因为CCRS 的坐标是基于hg19的,所以这里是hg19,ccrs就是-protocol参数里的标识符了,然后以.txt作为后缀。
然后是修改格式,一开始我用的方法是参考annovar提供的region-based数据库的格式,然后修改CCRS的格式。后来我发现这是行不通的,因为现成的数据库格式差别有点大,那么就只能看源码了。但其实我是不会perl的,在师姐的帮助下,完美的解决了这个问题。
虽然我们是使用table_annovar.pl进行注释的,实际上对于region-based数据库的注释是调用annotate_variation.pl,所以需要修改annotate_variation.pl的源码。在2998行我们可以看到,其实对于不同region-based数据库,都是有预设的。
- annotation/2.png)
所以根据CCRS的格式,我们可以在这里添加一个预设语句块。
- annotation/3.png)
当然也可以根据最后一个else语句块修改CCRS的格式
- annotation/4.png)
从这个语句块可以看出来,只需要在CCRS原始文件前面添加一列内容,以tab隔开,就行,添加啥也都无所谓,这里就不赘述了。
S-CAP
由于是基于位点的,那么在-operation参数里面呢是f,然后呢从网上下载下来的文件,一共有八个文件(不同区域不同标准,可以参考论文),任意选取一个截取前十行,长这样。
- annotation/5.png)
这里我已经把名字修改了,如果大家有查看过filter-based数据库,大抵都是这个格式,染色染位置、起始位置、结束位置、参考碱基、突变碱基、要注释的内容(可以是多列),以tab隔开。这里可以发现,少了一列结束位置,那是因为论文只针对snp,所以不用start、end表示也可以,这里用一个简单的语句就可以解决这一点。
1 | awk -F "\t" '{print $1"\t"$2"\t"$2"\t"$3"\t"$4"\t"$5}' scap3cr.txt > hg19_scap3cr.txt |
但是注意,这样是不够的,如果你看了这个论文,你会发现,这是预测splicing区域有害性的打分,更重要的是,论文中对splicing区域的划分和annovar默认的aplicing区域是不一样的!!!
在annovar里头,splicing的区域是2bp,也就是图中的1和4.
- annotation/6.png)
但是论文中作者为了更好的预测有害性,用了整整100bp的长度(内含子外显子各50bp),所以仅仅用annovar默认的splicing区域大小就太浪费这个打分了,那怎么扩大这个范围呢?
其实如果仔细看annovar说明书我们会发现,在annotate_variation.pl的脚本中有一个参数--splicing_threshold,可以控制splicing的区域大小,默认是2,但是我们用的是table_annovar.pl的脚本进行注释,虽然是调用annotate_variation.pl,但是却没有了--splicing_threshold这个参数,看来又只能改源码了。
在table_annovar.pl第380行(不同版本可能不太一样),有这么一句话。
- annotation/7.png)
里面在调用annotate_variation.pl的时候,直接给了--splicing_threshold这个参数,只要把后面的数字改成50就好了(原来是2)。至于怎么建立索引可以参考这里,是否建立索引会影响注释速度,但不会影响结果。
至此,这一部分内容就完了,我在实践中也就是这么使用的,具体的根据需要可以好好读一读annovar的官网说明。
水平有限,要是存在什么错误请指出,可发送邮件至shiyuant@outlook.com!请大家多多批评指正,相互交流,共同成长,谢谢!!!
附(vep安装笔记)
1 | #由于我用的是ubuntu server 18.04,不同linux发行版本之间的安装可能存在差异 |
WGS分析笔记(4)- Call SNVs/indels
最近一直忙期末汇报和脚本编写,没来的及接着往下写文章,年前把这一块写了,然后再往下的分析流程就比较特异性了,做一步写一步那种,相对于这种已经常规化的流程(除了一些细节上的差异,别的都是大同小异的了),再往下的可能就不是很常规的分析手段了,不同的实验室有不同的分析方法,希望能够有大佬提点意见,多多交流。
“突变”区别
对于WGS的数据,在处理完bam文件以后,就是call variations了,之后所有的工作其实都是针对variations进行分析,那么说到变异呢,其实中文的“变异”在英文里对应多个单词,经常看到傻傻分不清,这里稍微区别一下。
mutation:核苷酸序列的永久性改变(来源于ACMG),在人群中小于1%或5%(来源于北大生物信息学公开课)
polymorphism:在人群中频率超过1%(来源于ACMG),或超过5%(来源于北大生物信息学公开课)
variation/variant:以上两个的总和(来源于北大生物信息学公开课)
变异类型
我们一般所说的variations主要有四大类:SNV,INDEL,SV,CNV。(有些call变异软件也会支持MNV的calling,但是我们很少考虑这一类变异)
SNV即单核苷酸位点变异(single nucleotide variants)
INDEL即小片段插入缺失(insertion and deletion)
SV即结构变异(structural variation)
CNV即拷贝数变异(copy number variation)
SNV与SNP
说到SNV,可能大家也经常看到SNP(single nucleotide polymorphism),同样是混淆使用,这俩其实还是有一些区别的,看到上面对变异的区分,其实也能看出这俩的区别来:
一般SNP是二态的,SNV没有这样的限制,如果在一个物种中该单碱基变异的频率达到一定水平(1%)就叫SNP,而频率未知(比如仅仅在一个个体中发现)就叫SNV,SNV包含SNP。
变异简述
人基因组通常有4.1 - 5.0M的变异,但是99.9%都是由SNV和short indel造成。
通常,一个人全基因组内会有约 3.6 - 4.4 M 个 SNVs,绝大数(大于 95%)的高频(群体中等位基因频率大于 5%)的 SNP 在 dbSNP中有记录,高频的SNP一般都不是致病的主要突变位点。
通常,一个人全基因组内会有约 600K 的 Indel(<50bp的插入缺失为small indel)。
编码区或剪接位点处发生的插入缺失都可能会改变蛋白的翻译。
SV
结构变异指的是在基因组上一些大的结构性的变异,比如大片段丢失(deletion)、大片段插入(insertion)、大片段重复(duplication)、拷贝数变异(copy number variants)、倒位(inversion)、易位(translocation)。一般来说,结构变异涉及的序列长度在1kb到3Mb之间。结构变异普遍存在于人类基因组中,是个人差异和一些疾病易感性的来源。结构变异还可能导致融合基因的发生,一些癌症已经证实和结构变异导致的基因融合事件有关。
CNV
拷贝数变异指的是基因组上大片段序列拷贝数的增加或者减少,可分为缺失(deletion)和重复(duplication)两种类型,是一种重要的分子机制。CNV能够导致孟德尔遗传病与罕见疾病, 同时与包括癌症在内的复杂疾病相关,因此对于染色体水平的缺失、扩增的研究已经成为疾病研究热点。
以上数据在不同的数据库或文献上可能有所差异,但相去不远,具体的变异分类以及分布就不详述,可参考一些文献,下面说说怎么进行其中的SNV和indel的检测。
以下我将提供两种分析方式的脚本(DeepVariant以及bcftools)和流程,为啥没有GATK?因为我觉得黄老师的这篇GATK分析流程写得已经很好了,大家可以参考一下。
Bcftools
与旧版的samtools+bcftools不同,作者为了避免bcftools和samtools的版本不同导致的不兼容,新版的bcftools可以自己完成call snv/indel的工作。
使用bcftools进行变异检测,一般分为三部曲,分别为三个模块mpileup、call、filter,当然,我们一般也不会分三步进行操作,而是使用管道(pipeline)进行编写脚本,这样能减少产生一些不必要的过程文件,同时提高自动化和效率,下面是我的实际使用脚本。
1 | $ bcftools mpileup --threads 12 -q 20 -Q 20 -Ou -f /your/path/of/reference /your/bamfile/after/sorted.merged.markdup | bcftools call --threads 12 -vm -Ov | bcftools filter --threads 12 -s FILTER -g 10 -G 10 -i "%QUAL>20 && DP>6 && MQ>50 && (DP4[2]+DP4[3])>4" > raw.tmp.vcf |
有几个点值得讨论一下,首先是mpileup的-q参数,这个和之前提到的samtools view的-q是一样的,前面的文章有大篇幅说过这个MAPQ的数值,20翻译过来的意思其实就是比对正确率99%。
filter中的-s是软过滤的意思,就是把不符合后面条件的variations打上标签,但不过滤掉;-g,-G这对参数是说,indel附近的indel或snp是不准确的,大多是假阳性,过滤掉,这里我设的10bp,这个值还是比较合理的;-i是保留后面符合条件的变异,刚好和-e相反,两者选其一,我这里用的-i编写过滤表达式
QUAL:基于Phred格式的表示ALT的质量,也可以理解为可靠性;可以理解为所call出来的变异位点的质量值。Q=-10lgP,Q表示质量值;P表示这个位点发生错误的概率。因此,如果想把错误率从控制在90%以上,P的阈值就是1/10,那lg(1/10)=-1,Q=(-10)*(-1)=10。同理,当Q=20时,错误率就控制在了0.01。这个参数其实和mpileup的-Q是重复的。
DP是碱基的覆盖深度,一般很多公司和课题组会选择10,但我这里选择的是6,本着宽进严出的原则,保留更多的阳性variations,10也是没有关系的。
MQ不同于MAPQ,是RMS Mapping Quality,公式定义如下:q指的是比对到这个参考基因组碱基上的比对质量,即MAPQ。参考之前说的,MAPQ设置为20,假设每个碱基的MAPQ都是20,则MQ为20。
- Call SNVs indels/MQ.png)
参考上一篇里的MAPQ分布可以看到,使用bwa mem后,其实大多数的reads的MAPQ都在60,这样的话,MQ最好也就是60,但是在40有一个小突起,对于MQ的筛选,大家的选择可以酌情而定,50是一个大家使用较多的阈值点。- Call SNVs indels/MAPQ%E5%88%86%E5%B8%83.png)
- Call SNVs indels/MAPQ%E7%B4%AF%E7%A7%AF%E5%88%86%E5%B8%83%E6%9B%B2%E7%BA%BF.png)
DP4分别是正反链上REF和ALT的深度,我用“DP4[2]+DP4[3]>4”筛选ALT的深度至少是5的variations。
那么,以上的脚本其实是符合单个样本进行分析的,但如果是家系样本进行分析,其实是有问题的,因为在call这一步的时候用-v参数只输出变异位点,在获得了三个人的vcf文件进行merge的时候,对于一些变异(这些变异只存在于三个人的某一个或某两个),你就不知道不存在的那个人身上,是因为无变异还是没有覆盖到reads。这不利于做trio分析。那么要克服这个问题只需要去掉-v参数即可。
然后进行merge,是在完成了一个家系的call snp/indel以后。
1 | $ bgzip -c -f -@ 12 var.flt.vcf > var.vcf.gz |
之后可以用bcftools对结果做一下统计处理
1 | ## 统计结果plot-vcfstats |
DeepVariant
谷歌提供了分别适用于WGS和WES的脚本,可供大家参考。我亲测了一下这个软件,速度有点慢……完全没有谷歌自己描述的那么快,做为尝鲜吧,把当时的脚本放上来,这里要特别感谢师姐的指导!虽然最后我也没打算用这个软件完成我的课题吧。
https://github.com/google/deepvariant/tree/r0.7/scripts
Deepvariant无需安装,直接拉docker下来就行,不然要是安装,这个环境配置怕是要折磨死人的。
1 | # docker安装,仅针对ubuntu用户 |
拉取一下docker就可以使用deepvariant了
1 | $ sudo docker pull dajunluo/deepvariant |
之后便可以用bcftools或者gatk进行merge,对于这一步可以参考上面的gatk链接或者bcftools步骤。
到了这一步就可以完了么?显然不是,你用上述两个方法或者参考黄老师的脚本用gatk得到的结果,如果你仔细看,就会发现。- Call SNVs indels/vcf.png)
这是什么鬼,这又是什么鬼,为什么有那么多的多等位位点,你要是去统计,会发现这样的多等位位点还挺多的,所以你还不能直接过滤。对于这些变异我们一般是不会考虑嵌合的,因为平均30X的WGS是没法检测出嵌合体的。那么对于这样的位点怎么去考虑分析呢?
比较便捷的方法就是用bcftools里面的norm工具了。
1 | $ bgzip -c -f -@ 12 merge.var.vcf > merge.var.vcf.gz |
这样,多等位位点就变成了二等位位点了,便于后续的分析。今天的内容就到这里了,下一篇就是注释以及各种过滤了。
水平有限,要是存在什么错误请指出,可发送邮件至shiyuant@outlook.com!请大家多多批评指正,相互交流,共同成长,谢谢!!!
WGS分析笔记(3)- bam文件的处理
上一篇记录了mapping这一步的软件选择,也讲到了对于sam文件如何考虑MAPQ的过滤,这篇我主要想记录一下bam文件在进行call variation之前的处理。
包括MAPQ的筛选等都是这个处理的一部分。
既然要处理bam文件,不得不提bam文件的格式。
处理生物信息的数据时会发现,文件有各种各样的格式,眼花缭乱,这也是我一开始接触课题接触分析流程时的感受。但是多和这些文件打交道以后,会发现,大多数的不同格式的文件其本质都是文本文件,为了某种特殊的处理或记录需要,按一定的规则记录信息。包括之前接触的fasta、fastq文件,也包括sam文件,以后后面步骤会接触到的vcf文件等。
bam文件是sam文件的二进制格式,这里贴一张图,来说明一下为什么要转换成bam文件来处理。
- bam文件的处理/%E5%A4%A7%E5%B0%8F.png)
可以看到,不经过处理的sam文件是非常大的,非常不利于存储和处理,而转换格式后的bam文件小很多,所以很多处理软件也是针对bam文件进行开发的。
包括bwa,bowtie2的输出文件,都是sam文件,但是sam文件具体是什么样子的,我这里不会展开来讲,一是因为官网说明书已经说的很清楚了,二是因为你随手一个百度、谷歌(如果你翻得动墙)就有很多很多的人发帖介绍,而内容大体都是类似的,我自认为也没有什么能比他们讲得更好的。但是了解这个文件的内容确实是非常重要的。
以
@开头的行记录了header信息,之后的行记录了每个reads的mapping信息,一般对于这样的sam文件我们要做的处理大体就是先转换为bam文件,进行sort,再进行merge,最后mark duplicates,并建立索引。接下来我将一步步介绍怎么去处理,以及为什么我是这么处理的。在开始之间先使用samtools对参考序列进行索引建立,作用是用于samtools软件快速识别,这一步也是一劳永逸的,只要不把索引文件删除。
1
2$ samtools faidx re.fa
# 得到索引文件:re.fa.fai首先是把sam文件转换成bam文件,我们通过samtools view来实现,代码如下:
1
2$ samtools view -S in.sam -b > out.bam
$ samtools view -b in.bam -S > out.sam但实际上,在真正的操作中,我们是不会保留sam文件的,甚至是不会产生sam文件的,因此,我们通常这么来写命令。
1
2
3
4
5$ bwa mem -t 12 -M -R "@RG\tID:W2018001\tPL:ILLUMINA\tLB:W2018001\tSM:W2018001" /your/path/of/reference/ucsc.hg19.fasta 1.fq.gz 2.fq.gz | samtools view -q 1 -Shb - > W2018001.bam
# 关于“|”之前的我就不解释了,看我上一篇简书
# -q 1 :筛选MAPQ用的,意为保留MAPQ >= 1的记录,上一篇简书中讨论过关于MAPQ的由来和分布,这里用“1”也是保险起见,但实际上没啥区别,后期处理上(vcf处理),我们会以更严格的阈值去过滤
# -h :表示保留header信息
# -S,-b:表示格式,S指的是sam格式,b指的是bam格式这样操作的好处是直接可以得到bam文件,不必占用大量的空间存储sam文件。如果你实在是需要sam文件也可以转换回去,但如果你只是想查看一下,也可以通过以下方式实现。还是很方便的。
1
$ samtools view -h xxx.bam | less
在测序的时候序列是随机打断的,所以reads也是随机测序记录的,进行比对的时候,产生的结果自然也是乱序的,为了后续分析的便利,将bam文件进行排序。事实上,后续很多分析都建立在已经排完序的前提下。关于排序可以通过以下命令完成。
1
2
3
4
5
6$ samtools sort -@ 6 -m 4G -O bam -o sorted.bam W2018001.bam
# @:线程数
# m:每个线程分配的最大内存
# O:输出文件格式
# o:输出文件的名字
# 输入文件放在最后接下来要做的是merge,这个不是所有的样本都需要做的!!!
之前有提到,WGS的数据比较大,对于一个样本可能有多对文件,一般有两个思路,一个是先对原始的fastq文件进行merge,一个是对后面的bam文件进行merge。那么我选用的是后者。实现脚本如下:
1
2
3
4
5
6$ samtools merge -@ 6 -c sorted.merged.bam *.sorted.bam
# @:线程数
# c:当输入bam文件的header一样时,最终输出一个header
# 当然也可以用-h file,定义你想要的header,file里的内容就是sam文件header的格式
# 第一个bam是输出的文件名,后面排列输入的文件名,我这里用了通配符‘*’,要保证该目录下‘.sorted.bam’结尾的都是你要输入的文件
# 当然也可以用-b file,file文件里罗列要merge的文件名,一行一个文件名下一步就是remove duplicates,为什么要进行这一步呢?先来说一下测序,我们都知道人的基因组是很庞大的(约30亿个碱基对),在测序的时候,先会把基因组的DNA序列通过超声震荡随机打断成150bp的片段,那么从概率上来讲,出现同样的片段(开始和结束位置都一样)的几率是极小的。但是由于PCR对某些位置有偏好的扩增,会导致一些一模一样的reads存在。这些reads其实是一个片段的扩增导致的,多出来的reads,对该区段突变的判断是没什么贡献的,如果不加处理,反而会大大增加那个位置的深度,导致某些结果的不准确。
如下图所示,箭头所指的reads,就是duplicates,我们一般采取的策略是标记或者去除,这样的话,下一步call variation的时候会不考虑这些reads。
- bam文件的处理/duplicates2.png)
关于这一步,有很多软件可以实现,比较多用的是picard和samtools rmdup。我这里用的是GATK包里集成的picard的MarkDuplicates。关于picard和samtools rmdup的效果其实大家可以自己试一下,我很早之前做过的试验是,samtools rmdup速度很快,但是去除的效果稍差。大家用的最多的也是picard。
1
2
3
4
5
6$ java -jar /you/path/of/gatk/gatk-package-4.0.10.1-local.jar \
MarkDuplicates \
-INPUT sorted.merged.bam \
-OUTPUT sorted.merged.markdup.bam \
-METRICS_FILE markdup_metrics.txt
# 也可以加上“REMOVE_DUPLICATES=true”来去除掉这些duplicates,不然就只是标记到了这一步基本上就处理的差不多了,可以进行call variation了,但是这里还有一步建立索引,这十分的重要!!!!
必须对bam文件进行排序后,才能进行index,否则会报错。建立索引后将产生后缀为.bai的文件,用于快速的随机处理。很多情况下需要有bai文件的存在,特别是显示序列比对情况下。建立索引很简单。
1
$ samtools index sorted.merged.markdup.bam
到了这一步就基本上完事了,可以通过IGV或tview来查看情况,这都需要建立索引,且索引文件和bam文件在同一个目录下。
1
2
3$ samtools tview sorted.merged.markdup.bam re.fa
# 可以用-p chr:pos(加在tview和sorted.merged.markdup.bam之间)指定要查看的位置
# 也可以进去后用敲‘g’输入`chr10:10,000,000' 或 `=10,000,000'查看指定的位置,敲'?'了解更多说明,q退出下图就是效果了,用“?”,打开左边的帮助界面,其中圆点表示正链比对,逗号表示负链比对,星号表示插入。不同的颜色代表不同的含义,具体怎么调看帮助框。要是觉得不好看的话可以用IGV查看。IGV的效果就是上图duplicates的效果。
- bam文件的处理/tview.png)
同时对于得到的bam文件也可以进行一下查看,对于bam的统计软件就更多了,我这里网罗了一些帖子上的推荐以及我自己日常使用的软件,感兴趣的可以自己去下载来使用一下。
###samtools
这是个强大的软件,也自带一些统计工具,上篇简书其实我们就用到了,主要是四个:idxstats,depth,stats,flagstat
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45$ samtools depth sorted.merged.markdup.bam
示例结果
#chr pos depth
chr1 1 5
结果可以得到染色体名称、位点位置、覆盖深度
-a:输出所有位点,包括零深度的位点
-a -a --aa:完全输出所有位点,包括未使用到的参考序列
-b FILE:计算BED文件中指定位置或区域的深度
-f FILE:指定bam文件
-l INT:忽略小于此INT值的reads
-q INT:只计算碱基质量大于此值的reads
-Q INT:只计算比对质量大于此值的reads
-r CHR:FROM-END:只计算指定区域的reads
$ samtools idxstats sorted.merged.markdup.bam #需要预先进行sort和index
示例结果
#ref sequence_length mapped_reads unmapped_reads
chr1 195471971 6112404 0
结果可看出,分别统计染色体名称、序列长度、mapped数目,以及unmapped数目
$ samtools flagstat sorted.merged.markdup.bam
示例结果:
20607872 + 0 in total (QC-passed reads + QC-failed reads) #总共的reads数
0 + 0 duplicates #重复reads的数目
19372694 + 0 mapped (94.01%:-nan%) #总体上reads的数目以及匹配率;可能有有小偏差
20607872 + 0 paired in sequencing #paired reads的数目
10301155 + 0 read1 #reads1的数目
10306717 + 0 read2 #reads2的数目
11228982 + 0 properly paired (54.49%:-nan%) #完美匹配的reads数:比对到同一条参考序列,并且两条reads之间的距离符合设置的阈值
18965125 + 0 with itself and mate mapped#两条都比对到参考序列上的reads数,但是并不一定比对到同一条染色体上
407569 + 0 singletons (1.98%:-nan%)#只有一条比对到参考序列上的reads数,和上一个相加,则是总的匹配上的reads数。
3059705 + 0 with mate mapped to a different chr#两条分别比对到两条不同的染色体的reads数
1712129 + 0 with mate mapped to a different chr (mapQ>=5)#两条分别比对到不同染色体的且比对质量值大于5的数量
# 说明:
1.bwa的mem比对方法生成的bam文件保留sencondly比对的结果。所以使用flagstat给出的结果会有偏差。
2.每一项统计数据都由两部分组成,分别是QC pass和QC failed,表示通过QC的reads数据量和未通过QC的reads数量。以“PASS + FAILED”格式显示
$ samtools stats sorted.merged.markdup.bam
# 对bam文件进行详细的统计,也可只统计某一染色体的某一区域chr:from-to
结果包括:
Summary Numbers,raw total sequences,filtered sequences, reads mapped, reads mapped and paired,reads properly paired等信息
Fragment Qualitites #根据cycle统计每个位点上的碱基质量分布
Coverage distribution #深度为1,2,3,,,的碱基数目
ACGT content per cycle #ACGT在每个cycle中的比例
Insert sizes #插入长度的统计
Read lengths #read的长度分布
stats出来的结果可以使用plot-bamstats来画图(samtools目录下misc目录中)
$ plot-bamstats -p outdir/ sorted.merged.markdup.bam.stats下图就是plot-bamstats操作的输出结果了,可以看到有很多的图。效果还是很好的。
- bam文件的处理/plot-bamstats.png)
更多关于samtools的工具以及上文提到的工具的其余参数请参考官网:http://www.htslib.org/doc/samtools.html
###RSeQC
- 这也是上篇中提到过的,所以安装方式和使用就不赘述了,其实里面还有一些其余实用的工具,当然这款软件的最初使用对象是RNA-seq,但并不影响使用,有些工具是通用的,有一点要注意的是,bam_stat.py里的unique mapping的默认阈值是MAPQ>=30,当然可以通过参数来修改,这个在结果的理解上大家要注意。
###bedtools
这是一个经常使用也很实用的软件,我经常会用来截取bam然后在igv上看突变的情况,师姐推荐其中的mutlicov进行覆盖度的统计。我粗略的看了一下bedtools的说明书,用于coverage统计的应该还有coverage,genomecov。感兴趣的可以尝试一下。
1
2
3
4
5
6
7
8bedtools:
$ wget https://github.com/arq5x/bedtools2/releases/download/v2.27.1/bedtools-2.27.1.tar.gz
$ tar -zxvf bedtools-2.27.1.tar.gz
$ cd bedtools2
$ make
# 脚本在bin/下的bedtools
# Ubuntu用户也可以使用下述命令来下载:
$ sudo apt-get install bedtools截取bam文件,查看igv可以用以下命令:
1
2
3
4
5$ bedtools intersect -a sorted.merged.markdup.bam -b region.sorted.bed > target_reads.bam && samtools index target_reads.bam
#其中bed文件的格式可以参考:
#染色体号 起始位置 终止位置
chr1 226173187 226173247
#用"\t"分隔
###GATK
- GATK不仅可以call variation,里面还包含了很多其他用途的工具包,其中有一个工具叫DepthOfCoverage,可以统计depth和coverage,但是在panel中比较适用,因为有bed范围,且比较小。这个工具的速度是比较慢的,要在全基因组上做不太现实。所以我本人也没去使用。
###BAMStats
- 一款比较早的bam统计软件,没用过,但是看说明使用是极其简单了,说一下怎么安装。感兴趣的可以自己试一下,很简单。
1
2$ wget https://jaist.dl.sourceforge.net/project/bamstats/BAMStats-1.25.zip
$ unzip BAMStats-1.25.zip
###bamdst
一款简单好用的深度统计软件。
1
2
3$ git clone https://github.com/shiquan/bamdst.git
$ cd bamdst/
$ make安装好后,需要准备.bed文件及.bam文件,以软件提供的MT-RNR1.bed和test.bam为例,使用命令如下:
1
$ bamdst -p MT-RNR1.bed -o ./ test.bam
输出的结果包含7个文件,为:
- -coverage.report
- -cumu.plot
- -insert.plot
- -chromosome.report
- -region.tsv.gz
- -depth.tsv.gz
- -uncover.bed
主要看一下coverage.report文件,里面包含了大量信息。
###qualimap
这算是压轴了吧,这个软件是我师姐推荐的,安装使用都比较容易,给出的是PDF或HTML的报告,报告中的信息特别丰富,还有一堆的图,所以在我自己的脚本中也会对每个样本使用该软件统计,简述一下安装和使用。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24# 第一步:下载
$ mkdir qualimap
$ cd qualimap
$ wget https://bitbucket.org/kokonech/qualimap/downloads/qualimap_v2.2.1.zip
$ unzip qualimap_v2.2.1.zip
$ cd qualimap_v2.2.1
# 第二步安装相关的软件
# java
# 这个应该都有,这里就是贴一下官网的步骤
$ sudo apt-get install openjdk-6-jre
# R
# 官网上也有,我贴的是自己以前安装的记录
$ apt-key adv --keyserver keyserver.ubuntu.com --recv-keys E298A3A825C0D65DFD57CBB651716619E084DAB9
$ apt-get update
$ apt-get install r-base
$ apt install r-base-core
# R包安装,两个方法,第一个听说容易报错,我用的是第二个
$ Rscript scripts/installDependencies.r
# 或
$ R
> install.packages("optparse")
> source("http://bioconductor.org/biocLite.R")
> biocLite(c("NOISeq", "Repitools", "Rsamtools", "GenomicFeatures", "rtracklayer"))
> q()使用也简单,主要分为带gtf文件和不带gtf文件,全基因组的话一般不带gtf文件,然后bamqc其实也只是这个软件中的一个工具,其他的工具感兴趣的也可以看看。
1
2$ qualimap bamqc -bam sorted.merged.markdup.bam --java-mem-size=20G -c -nt 16 -outdir bamqc -outfile bamqc.pdf -outformat PDF:HTML
# 参数也没有什么特别要注意的,基本上默认的就可以找了一个示例结果,发现有23页,我这里就不贴了,大家可以自己尝试一下。
最后贴两张图,是我自己写的脚本得到的深度分布,累积曲线以及覆盖率,因为是自己写的,所以比较糙,横纵坐标标题什么的一律没写。
- bam文件的处理/depth.png)
上图可以看到,深度分布还是比较正态的,最多的30X左右,至于左边0X为什么这么高,是因为参考基因组有些位置就是N,还有一些位置就是我的样本没有覆盖到。
- bam文件的处理/depth.cdf.png)
上图可以看到,小于10X的数据的不到2%,超过50%的数据都是高于30X的,还是不错的。
- bam文件的处理/coverage.png)
上图我按不同的染色体进行统计覆盖率,去掉了其余的一些未知染色体位置的序列上的信息(这个信息具体要了解参考基因组的特性,比如有些序列目前能明确在人身上,却不知道具体在哪个染色体等,这些信息也是包含在参考基因组中的,仔细看参考基因组会发现,除了22条常染色体,2条性染色体,还有很多其他的序列),这个覆盖率并不是我想想的那般全体高于99%,也没公司给的报告描述的那么好,主要是因为MAPQ的过滤导致了这样的结果,但是总体的覆盖率还可以。
水平有限,要是存在什么错误请指出,可发送邮件至shiyuant@outlook.com!请大家多多批评指正,相互交流,共同成长,谢谢!!!
WGS分析笔记(2)- bwa vs bowtie2
在进行正式的mapping记录之前,先记录一下bwa与bowtie2在mapping这个环节的情况。
一般对于WGS结果的mapping,一般推荐的软件有两款,分别是bwa和bowtie2,大多数的公司报告或者网上的教程,我所看到的都是使用bwa进行比对的,这里,我来进行一下两个软件的对比。
实验对象还是之前文章提到的那个样本的数据,我只取用其中的一对数据进行mapping并比较。
比较之前先进行一下软件安装、参考序列下载并建立索引
1
2
3
4
5
6
7
8
9bowtie2
$ wget https://sourceforge.net/projects/bowtie-bio/files/bowtie2/2.3.4.3/bowtie2-2.3.4.3-linux-x86_64.zip
# https://sourceforge.net/projects/bowtie-bio/files/bowtie2/2.3.4/bowtie2-2.3.4-linux-x86_64.zip
$ unzip bowtie2-2.2.9-linux-x86_64.zip
$ ln -sf /biosoft/bowtie2-2.3.4.3-linux-x86_64/bowtie2 /home/shiyuantong/bin/bowtie2
BWA:
$ wget https://sourceforge.net/projects/bio-bwa/files/bwa-0.7.17.tar.bz2
$ tar -jxvf bwa-0.7.17.tar.bz2 # x extracts, v is verbose (details of what it is doing), f skips prompting for each individual file, and j tells it to unzip .bz2 files
$ make关于安装这里有一些需要注意的地方!!!!!
首先是bowtie2,建议大家使用2.3.4的下载链接,我在下载的时候最新版是2.3.4.3,但是在使用的出现了报错!!!!!
报错的内容如下(当时没截图):
Segmentation fault (core dumped) (ERR): bowtie2-align exited with value 139这个报错只会出现在批量处理的脚本中,对单个样本的处理并没有影响,但是实际使用的时候,大家都是批量处理样本,怎么可能一个样本一个命令,因此推荐2.3.4的版本,当然,下面的比较不会涉及这个问题。
还有就是BWA了,这个软件ubuntu用户也可以直接使用
sudo apt-get install bwa命令进行安装,我看了一下,两种方法的版本是一致的,都是0.7.17。然后是参考序列,这里直接使用ucsc的hg19,下载与建立索引方式如下,根据自己的需要调整目录
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17hg19:
$ cd /your/path/of/reference/
$ wget http://hgdownload.cse.ucsc.edu/goldenPath/hg19/bigZips/chromFa.tar.gz
$ tar zvfx chromFa.tar.gz
$ cat *.fa > hg19.fa
$ rm chr*.fa
建立bwa索引:
$ bwa index -a bwtsw hg19.fa
# 产生.bwt .pac .ann .amb .sa五个新文件
# -a:两种构建index算法,bwtsw以及is,bwtsw适用大于10MB的参考基因组,比如人,is适用于小于2GB的数据库,是默认的算法,速度较快,需要较大的内存,
# -p:输出数据库的前缀,默认与输入文件名一致,这里我没有加这个参数,直接输出到当前目录
建立bowtie2索引:
$ bowtie2-build hg19.fa hg19.fa
# bowtie2-build命令在安装bowtie2的目录下找到
# 第一个hg19.fa代表输入的参考序列
# 第二个hg19.fa代表输出的索引文件前缀
# 产生六个.bt2新文件上述程序建立索引速度较慢,尤其是bowtie2,但是一次建好,一劳永逸,请大家耐心等待,也可以放在后台,防止终端突然的中断。
建立好索引就可以直接开始比对了,以下是我的比对程序,都开了24线程,用
nohup …… &放在后台运行,用time记录时间。1
2$ nohup time bowtie2 -p 24 -x /your/path/of/reference/ucsc.hg19.fasta --rg-id W2018001 --rg PL:ILLUMINA --rg LB:W2018001 --rg SM:W2018001 -1 W2018001_NZTD180602206_HCV5MDMXX_L1.cleaned.1.fq.gz -2 W2018001_NZTD180602206_HCV5MDMXX_L1.cleaned.2.fq.gz -S W2018001.bowtie2.sam > W2018001.bowtie2.log &
$ nohup time bwa mem -t 24 -M -R "@RG\tID:W2018001\tPL:ILLUMINA\tLB:W2018001\tSM:W2018001" /your/path/of/reference/ucsc.hg19.fasta W2018001_NZTD180602206_HCV5MDMXX_L1.cleaned.1.fq.gz W2018001_NZTD180602206_HCV5MDMXX_L1.cleaned.2.fq.gz 1>W2018001.bwa.sam 2>W2018001.bwa.log &这一步会比较久,我也是经过漫长的半天等待终于迎来了结果,首先看一下速度吧。先前的脚本使用了
time的命令,可以直接看到速度,在日志文件里。- bwa vs bowtie2/%E6%97%B6%E9%97%B4%E5%AF%B9%E6%AF%94.png)
日志文件的最后两行就是
time命令输出的结果,所以没有必要用cat查看,而且bwa的日志文件,要是用cat怕是屏幕要炸。图中可以看到两个红色的框,就是我标出来的时间。(其实我原来用time命令,结果不长这样的,这个结果不太利于观看,但是也能说明问题了)很明显的可以看到半套全基因组的数据(我只用了样本一半的数据)bowtie2跑的更快一些,但其实大家不用纠结这个点。因为上一次我用24线程,一样的脚本一样的数据,跑bowtie2花了六个多小时,速度没有bwa快,同时以前在使用酵母的测序数据(数据量会比较小)的时候,明显发现bwa速度比bowtie2快,甚至在说法上你也会发现不同的人给你的说法是不一样的,有些人说bwa快有些人说bowtie2快,网上看帖子也没有一个十分明确的说法哪个速度快。这里大家完全可以用自己的数据和脚本跑一下,看看结果。
接下来我想看看比对效果,这里我先采用了samtools的flagstat分别进行统计,下面是安装samtools的步骤:
1
2
3
4
5
6
7
8samtools:
$ wget https://github.com/samtools/samtools/releases/download/1.9/samtools-1.9.tar.bz2
$ tar xvfj samtools-1.9.tar.bz2
$ cd samtools-1.9
$ ./configure --prefix=/where/to/install
$ make
$ make install
# samtools其实我到现在为止装的最崩溃的软件之一了,因为在实际安装的时候你会发现它需要各种各样的库的支持,对于使用新机器的我,我基本是安装,报错缺什么库,安装缺的库,重新安装,这么折腾了一下午接下来就是使用统计工具,其实很简单。
1
2$ samtools flagstat W2018001.bowtie2.sam >W2018001.bowtie2.flagstat
$ samtools flagstat W2018001.bwa.sam >W2018001.bwa.flagstat这个也需要花一点时间,但不会太长,看一下结果。
- bwa vs bowtie2/flagstat.png)
这个结果还是比较清楚的,bwa的结果比bowtie2稍稍好一点。但相差不是很大,所以对于这两个软件,一直是公说公有理,婆说婆有理,这里我用另一个软件对结果进行统计,再进行对比试试。
RSeQC是一个功能强大的软件,里面有很多实用的小工具,其中的bam_stat就是一个实用的bam/sam结果统计工具,安装方式也是相当简单了,就是一个python的包,支持python2.x和python3.x,这里我选用python3的pip来安装,因为本人习惯使用python3。
1
$ pip3 install RSeQC
使用和结果如下,由于我这个sam文件比较大,运行起来比较慢,所以我开了俩终端。
- bwa vs bowtie2/bam_stat.png)
其实我最想看的unique mapping的reads,因为后期为了降低假阳性,在处理bam文件的时候会选择unique mapped的reads,但是在查看说明书无果后,找遍论坛没有找到一个能够说服我的筛选unique mapped的方式。
有这么几个方式,一个说是看tag,但是bwa的结果,你仔细看说明书和结果,会发现,这个tag并没有什么用,bowtie2倒是还可以。
第二个也是说的比较多的一个,看MAPQ。那么mapq是啥呢,我来贴几张图。
- bwa vs bowtie2/bowtie2%E7%9A%84%E8%AF%B4%E6%98%8E.png)
- bwa vs bowtie2/SAM%E7%9A%84%E8%AF%B4%E6%98%8E.png)
- bwa vs bowtie2/%E5%AE%98%E7%BD%91%E8%AF%B4%E6%98%8E.png)
- 分别是sam格式官网的说明,bowtie2官网的说明,这两个说明的公式是一样的,都指向最后一个官网的说明。看到这个官网的公式,我直接就傻掉了,反正到现在也没推出个所以然来。但是前两张图就很好理解了。但是和很多人说的MAPQ>=1就是unique mapping,我觉得是对不上的。对于这点我不多说,这里的解释也是目前为止我最能接受的。
- 那上面那个结果,bam_stat,我在阅读源码后,发现是以MAPQ>=30作为阈值来挑选是否unique的。由于bwa和bowtie2的mapq的计算方式不一样,这个结果其实并不可信。于是我写了一个脚本,看了一下mapq的分布情况。
- bwa vs bowtie2/bowtie2.png)
- bwa vs bowtie2/bwa.png)
这个图能说明什么呢,有待商榷。
这个时候再回过来看一下bowtie2的输出结果和大家说的bowtie2的筛选unique mapping的方法以及结果。
- bwa vs bowtie2/bowtie2.log.png)
- bwa vs bowtie2/bowtie2_tag.png)
其实到这里我也不知道该怎么办了,到现在还是不知道,bwa结果用mapq>=1是否能得到unique mapping。这个结果对于后续分析影响有多大我不好说,至于怎么选择,我也不发表意见,不过在后续的筛选中,gatk给出的建议是mapq>=40。
2019-1-9补充bwa结果,按mapq分布,分别计算>=1,10,20,30的比例。为大家选择MAPQ作为筛选提供一个参考。
- bwa vs bowtie2/mapq%E5%88%86%E5%B8%83.png)
但是回归主题,bwa和bowtie2,我决定选择bwa。
水平有限,要是存在什么错误请指出,可发送邮件至shiyuant@outlook.com!请大家多多批评指正,相互交流,共同成长,谢谢!!!
- call CNV 和一些其他/1.png)
- call CNV 和一些其他/2.png)