python: numpy学习笔记

列表与array的区别

在实现层面，数组基本上包含一个指向连续数据块的指针。另一方面，Python列表包含一个指向指针块的指针，这其中的每一个指针对应一个完整的Python对象。另外，列表的优势是灵活，因为每个列表元素是一个包含数据和类型信息的完整结构体，而且列表可以用任意类型的数据填充。固定类型的NumPy式数组缺乏这种灵活性，但是能更有效地存储和操作数据。

导入numpy

1	import numpy as np

array的创建

从列表创建数组

通过 list 创建一维 array

list1 = [1,3,5,7]
nd1 = np.array(list1)
print(nd1)
print(type(nd1))

[1 3 5 7]
<class 'numpy.ndarray'>

通过 list 创建二维 array

list2 = [[1,2,4,8],[4,5,9,3]]
nd2 = np.array(list2)
print(nd2)
print(type(nd2))

[[1 2 4 8]
 [4 5 9 3]]
<class 'numpy.ndarray'>

如果需要明确数组的数据类型，可以用dtype关键字

1	np.array([1, 3, 4], dtype='float32')

array([1., 3., 4.], dtype=float32)

从头创建数组

通过范围创建 array

# 线性序列
# 从10开始，1结束（不包含），步长为-1
# arange([start,]stop[,step],dtype=None)
np.arange(10, 1, -1)

array([10,  9,  8,  7,  6,  5,  4,  3,  2])

1 2	# 创建五个元素的数组，这5个数均匀地分配到0-1 np.linspace(0, 1, 5)

array([0.  , 0.25, 0.5 , 0.75, 1.  ])

生成特殊矩阵

1
2
3

# 全零矩阵
np.zeros((2,3))
np.zeros(5, dtype=int)

array([0, 0, 0, 0, 0])

1
2
3

# 全一矩阵
np.ones((4,4), dtype=float)
np.ones(5)

array([1., 1., 1., 1., 1.])

1 2	# 默认值一直的矩阵 np.full((3, 5), 3.4)

array([[3.4, 3.4, 3.4, 3.4, 3.4],
       [3.4, 3.4, 3.4, 3.4, 3.4],
       [3.4, 3.4, 3.4, 3.4, 3.4]])

1 2	# 单位矩阵 np.eye(3)

array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

1 2	# 对角线矩阵 np.diag([1,2,3,4])

array([[1, 0, 0, 0],
       [0, 2, 0, 0],
       [0, 0, 3, 0],
       [0, 0, 0, 4]])

1
2
3

# 创建一个由3个整型数组成的未初始化的数组
# 数组的值是内存空间中的任意值
np.empty(3)

array([1., 1., 1.])

生成随机数组
- random生成0到1之间的随机数
- uniform生成均匀分布随机数
- randn生成标准正态的随机数
- normal生成正态分布
- shuffle随机打乱顺序
- seed设置随机种子数

1 2	# 设计随机种子 np.random.seed(123)

1
2
3

# 创建一个3*3、在0-1均匀分布的随机数组成的数组
x = np.random.random((3,3))
print(x)

[[0.69646919 0.28613933 0.22685145]
 [0.55131477 0.71946897 0.42310646]
 [0.9807642  0.68482974 0.4809319 ]]

1
2
3

# 打乱随机数
np.random.shuffle(x)
print(x)

[[0.9807642  0.68482974 0.4809319 ]
 [0.69646919 0.28613933 0.22685145]
 [0.55131477 0.71946897 0.42310646]]

1 2	# 创建一个3*3的、均值为0，方差为1的正态分布的随机数数组 np.random.normal(0, 1, (3, 3))

array([[ 1.26593626, -0.8667404 , -0.67888615],
       [-0.09470897,  1.49138963, -0.638902  ],
       [-0.44398196, -0.43435128,  2.20593008]])

1 2	# 创建一个3*3，[0, 10)区间的随机整型数组 np.random.randint(0, 10, (3, 3))

array([[8, 0, 7],
       [9, 3, 4],
       [6, 1, 5]])

Numpy数据类型

指定方式

字符串

dtype='int16'
numpy对象

dtype=np.int16

数据类型
数据类型:描述
- bool_:布尔值（真、True 或假、False），用一个字节存储
- int_ : 默认整型（类似于 C 语言中的 long，通常情况下是 int64 或 int32）
- intc_ : 同 C 语言的 int 相同（通常是 int32 或 int64）
- intp : 用作索引的整型（和 C 语言的 ssize_t 相同，通常情况下是 int32 或 int64）
- int8 : 字节（byte，范围从–128 到 127）
- int16 : 整型（范围从–32768 到 32767）
- int32 : 整型（范围从–2147483648 到 2147483647）
- int64 : 整型（范围从–9223372036854775808 到 9223372036854775807）
- uint8 : 无符号整型（范围从 0 到 255）
- uint16 : 无符号整型（范围从 0 到 65535）
- uint32 : 无符号整型（范围从 0 到 4294967295）
- uint64 : 无符号整型（范围从 0 到 18446744073709551615）
- float_ : float64 的简化形式
- float16 : 半精度浮点型：符号比特位，5 比特位指数（exponent），10 比特位尾数（mantissa）
- float32 : 单精度浮点型：符号比特位，8 比特位指数，23 比特位尾数
- float64 : 双精度浮点型：符号比特位，11 比特位指数，52 比特位尾数
- complex_ : complex128 的简化形式
- complex64 : 复数，由两个 32 位浮点数表示
- complex128 : 复数，由两个 64 位浮点数表示

查看属性

1 2	# shape nd2.shape

(2, 4)

1 2	# size 元素的个数 nd2.size

1 2	# 数据类型 nd2.dtype

dtype('int32')

1 2	# 数组的维度 nd2.ndim

1 2	# 每个数组元素字节大小 nd2.itemsize

1
2
3

# 数组总字节大小
# 一般认为 nbytes 跟 itemsize 和 size 的乘积大小相等
nd2.nbytes

数据的索引

获取单个元素

对于一维数组，直接通过中括号指定索引获取第i个值（从0开始计数）
1
x[1]
用负值索引末尾索引
1
x[-1]
多维数组中，可以用逗号分隔的索引元组获取元素
1
x[2, -1]
用以上索引方式修改元素值
1
x[0, 0] = 12

NumPy 数组是固定类型的。这意味着当你试图将一个浮点值插入一个整型数组时，浮点值会被截短成整型。并且这种截短是自动完成的，不会给你提示或警告，所以需要特别注意这一点！

数据的切片

1	x[start:stop:step]

当上述参数均未指定，那么缺省值为：start = 0、stop = 维度的大小（size of dimension） 和 step = 1
一维数组

1
2
3

import numpy as np
x = np.arange(10)
x[:5] # 前五个元素

array([0, 1, 2, 3, 4])

1	x[5:] # 索引5以后的元素

array([5, 6, 7, 8, 9])

1	x[4:7] # 索引4到6

array([4, 5, 6])

1	x[::2] # 隔一个元素

array([0, 2, 4, 6, 8])

1	x[::-1] # 逆序取所有元素

array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])

1	x[5::-2] # 从索引5隔一个逆序

array([5, 3, 1])

多维子数组

1 2	x2 = np.array([range(1 + i, 5 + i) for i in range(5)]) x2[:2, :3] # 两行三列

array([[1, 2, 3],
       [2, 3, 4]])

1	x2[:, ::2] # 所有行，隔一列

array([[1, 3],
       [2, 4],
       [3, 5],
       [4, 6],
       [5, 7]])

1	x2[::-1, ::-1] # 逆序

array([[8, 7, 6, 5],
       [7, 6, 5, 4],
       [6, 5, 4, 3],
       [5, 4, 3, 2],
       [4, 3, 2, 1]])

行、列获取

一个冒号（:）表示空切片

1	x2[:, 1] # 第二列

array([2, 3, 4, 5, 6])

1	x2[1, :] # 第二行

array([2, 3, 4, 5])

1	x2[1] # 行的简便写法

array([2, 3, 4, 5])

非副本视图的子数组

是数组切片返回的是数组数据的视图，而不是数值数据的副本
意思就是说，当修改子数组的数据时，原数据也会被修改
它意味着在处理非常大的数据集时，可以获取或处理这些数据集的片段，而不用复制底层的数据缓存

创建数组的副本

通过copy()来完成复制数组里的数据或者子数组

1	x_sub = x2[:2, :2].copy()

数据的变形

通过reshape()实现数组变形

1	np.arange(1, 10).reshape((3, 3))

原始数组的大小和变形后数组的大小一致
如果不能保证上述条件，-1表示自动填充位置的维度
1
np.arange(1, 10).reshape((3, -1))
使用newaxis将一个一维数组转变为二维的行或列的矩阵
1
2
3
4
# 行矩阵
x[np.newaxis, :]
# 列矩阵
x[:, np.newaxis]

数组的拼接和分裂

数组的拼接

np.concatenate
- 以数组元组或数组列表作为第一个参数

# 拼接两个数组
x = np.array([1, 2, 3])
y = np.array([3, 2, 1])
np.concatenate([x, y])

array([1, 2, 3, 3, 2, 1])

1
2
3

# 拼接多个数组
z = [11, 11, 11]
np.concatenate([x, y, z])

array([ 1,  2,  3,  3,  2,  1, 11, 11, 11])

# 二维数组拼接
# 按第一个轴拼接，上下拼接
grid = np.array([range(1 + i, 5 + i) for i in range(3)])
np.concatenate([grid, grid])

array([[1, 2, 3, 4],
       [2, 3, 4, 5],
       [3, 4, 5, 6],
       [1, 2, 3, 4],
       [2, 3, 4, 5],
       [3, 4, 5, 6]])

1 2	# 按第二个轴拼接，左右拼接 np.concatenate([grid, grid], axis = 1)

array([[1, 2, 3, 4, 1, 2, 3, 4],
       [2, 3, 4, 5, 2, 3, 4, 5],
       [3, 4, 5, 6, 3, 4, 5, 6]])

np.vstack 垂直栈

1	np.vstack([x, y])

array([[1, 2, 3],
       [3, 2, 1]])

np.hstack 水平栈

1	np.hstack([x, y])

array([1, 2, 3, 3, 2, 1])

np.dstack 沿着第三个维度拼接数组

1	np.dstack([x, y])

array([[[1, 3],
        [2, 2],
        [3, 1]]])

数组的分裂

与拼接相反的过程，通过np.split、np.hsplit和np.vsplit来实现
传递一个索引列表作为参数，索引列表记录的是分裂点位置
N个分裂点会得到 N + 1 个子数组

np.split

1 2	x = [1, 2, 3, 4, 5, 6, 7] np.split(x, [3, 5])

[array([1, 2, 3]), array([4, 5]), array([6, 7])]

np.vsplit()

1 2	grid = np.arange(16).reshape((4,-1)) np.vsplit(grid, [2])

[array([[0, 1, 2, 3],
        [4, 5, 6, 7]]), array([[ 8,  9, 10, 11],
        [12, 13, 14, 15]])]

np.hsplit()

1	np.hsplit(grid, [2])

[array([[ 0,  1],
        [ 4,  5],
        [ 8,  9],
        [12, 13]]), array([[ 2,  3],
        [ 6,  7],
        [10, 11],
        [14, 15]])]

np.dsplit()

数组沿着第三个维度分裂
通用函数

向量操作
- 通过简单地对数组执行操作来实现，这里对数组的操作将会被用于数组中的每一个元素

数组的运算

运算符	通用函数	描述
+	np.add	加法
-	np.subtract	减法
-	np.negative	负数
*	np.multiply	乘法
/	np.divide	除法
//	np.floor_divide	地板除/求整数
**	np.power	指数运算
%	np.mod	模/余数

绝对值

可以识别内置abs()函数
对应np.absolute函数
别名np.abs
处理复数时返回复数的幅度
三角函数

# 三角函数
theta = np.linspace(0, np.pi, 3)
print('theta      = ', theta)
print('sin(theta) = ', np.sin(theta))
print('cos(theta) = ', np.cos(theta))
print('tan(theta) = ', np.tan(theta))

theta      =  [0.         1.57079633 3.14159265]
sin(theta) =  [0.0000000e+00 1.0000000e+00 1.2246468e-16]
cos(theta) =  [ 1.000000e+00  6.123234e-17 -1.000000e+00]
tan(theta) =  [ 0.00000000e+00  1.63312394e+16 -1.22464680e-16]

# 反三角函数
x = [-1, 0, 1]
print('x         = ', x)
print('arcsin(x) = ', np.arcsin(x))
print('arccos(x) = ', np.arccos(x))
print('arctan(x) = ', np.arctan(x))

x         =  [-1, 0, 1]
arcsin(x) =  [-1.57079633  0.          1.57079633]
arccos(x) =  [3.14159265 1.57079633 0.        ]
arctan(x) =  [-0.78539816  0.          0.78539816]

指数和对数

自然数的指数运算：np.exp
2的指数运算：np.exp2
自定义的指数运算：np.power
自然数为底的对数运算：np.log
2为底的对数运算：np.log2
10为底的对数运算：np.log10
以任意数为底的对数运算：np.log(m)/np.log(n)
- m 为底数
- n 为真数

# 指数运算
x = [1, 2, 3, 4]
print('x    =', x)
print('e^x  =', np.exp(x))
print('2^x  =', np.exp2(x))
print('3^x  =', np.power(3, x))

x    = [1, 2, 3, 4]
e^x  = [ 2.71828183  7.3890561  20.08553692 54.59815003]
2^x  = [ 2.  4.  8. 16.]
3^x  = [ 3  9 27 81]

# 对数运算
print('ln(x)    =', np.log(x))
print('log2(x)  =', np.log2(x))
print('log10(x) =', np.log10(x))

ln(x)    = [0.         0.69314718 1.09861229 1.38629436]
log2(x)  = [0.        1.        1.5849625 2.       ]
log10(x) = [0.         0.30103    0.47712125 0.60205999]

# 对于非常小的输入值的更好精度计算
x = [0, 0.001, 0.01, 0.1]
print('exp(x) - 1 =', np.expm1(x))
print('log(1 + x) =', np.log1p(x))

exp(x) - 1 = [0.         0.0010005  0.01005017 0.10517092]
log(1 + x) = [0.         0.0009995  0.00995033 0.09531018]

logaddexp(a, b)，在计算log(exp(a) + exp(b)) 更准确

高级的通用函数特性

指定输出

在进行大量运算时，有时候指定一个用于存放运算结果的数组是非常有用的。不同于创建临时数组，你可以用这个特性将计算结果直接写入到你期望的存储位置。所有的通用函数都可以通过 out 参数来指定计算结果的存放位置

# 指定计算结果的存放位置
x = np.arange(5)
y = np.empty(5)
np.multiply(x, 10, out = y)
print(y)

[ 0. 10. 20. 30. 40.]

# 写入指定数组的每隔一个元素的位置
y = np.zeros(10)
np.power(2, x, out=y[::2])
print(y)

[ 1.  0.  2.  0.  4.  0.  8.  0. 16.  0.]

聚合

reduce：望用一个特定的运算 reduce 一个数组，那么可以用任何通用函数的 reduce 方法。一个 reduce 方法会对给定的元素和操作重复执行，直至得到单个的结果

x = np.arange(1, 6)
y = np.add.reduce(x)
print(y)
z = np.multiply.reduce(x)
print(z)

15
120

accumulate: 存储每次计算的中间结果

y = np.add.accumulate(x)
print(y)
z = np.multiply.accumulate(x)
print(z)

[ 1  3  6 10 15]
[  1   2   6  24 120]

在一些特殊情况中，NumPy 提供了专用的函数（np.sum、np.prod、np.cumsum、np.cumprod ），它们也可以实现以上 reduce 的功能
外积
任何通用函数都可以用 outer 方法获得两个不同输入数组所有元素对的函数运算结果

y = np.multiply.outer(x, x)
print(y)
z = np.add.outer(x, x)
print(z)

[[ 1  2  3  4  5]
 [ 2  4  6  8 10]
 [ 3  6  9 12 15]
 [ 4  8 12 16 20]
 [ 5 10 15 20 25]]
[[ 2  3  4  5  6]
 [ 3  4  5  6  7]
 [ 4  5  6  7  8]
 [ 5  6  7  8  9]
 [ 6  7  8  9 10]]

聚合：最大值、最小值和其他值

求和
- 通过np.sum实现
- array.sum()可便捷调用
最大值
- 通过np.min实现
- array.min()可便捷调用
最小值
- 通过np.max实现
- array.max()可便捷调用

1. 多维度聚合

通过指定axis用于沿着某个轴的方向进行聚合。
    * axis = 0 表示每一列，即第一个轴被折叠
    * axis = 1 表示每一行，即第二个轴被折叠

M = np.random.random((3,4))
print(M)
print(M.sum())
print(M.min(axis=0))
print(M.max(axis=1))

[[0.36178866 0.22826323 0.29371405 0.63097612]
 [0.09210494 0.43370117 0.43086276 0.4936851 ]
 [0.42583029 0.31226122 0.42635131 0.89338916]]
5.022928013697376
[0.09210494 0.22826323 0.29371405 0.4936851 ]
[0.63097612 0.4936851  0.89338916]

2. 其他聚合函数

大多数的聚合都有对 NaN 值的安全处理策略（NaN-safe），即计算时忽略所有的缺失值，这些缺失值即特殊的 IEEE 浮点型 NaN 值

函数名称	NaN安全版本	描述
np.sum	np.nansum	计算元素的和
np.prod	np.nanprod	计算元素的积
np.mean	np.nanmean	计算元素的平均值
np.std	np.nanstd	计算元素的标准差
np.var	np.nanvar	计算元素的方差
np.min	np.nanmin	找出最小值
np.max	np.nanmax	找出最大值
np.argmin	np.nanargmin	找出最小值的索引
np.argmax	np.nanargmax	找出最大值的索引
np.median	np.nanmedian	计算元素的中位数
np.percentile	np.nanpercentile	计算基于元素排序的统计值
np.any	N/A	验证任何一个元素是否为真
np.all	N/A	验证所有元素是否为真

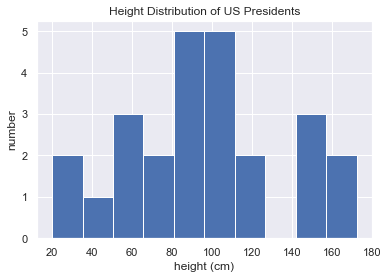
heights = np.random.random(25) * 175
print(heights)
print("Mean height: ", heights.mean())
print("Standard deviation:", heights.std())
print("Minimum height: ", heights.min())
print("Maximum height: ", heights.max())
print("25th percentile: ", np.percentile(heights, 25))
print("Median: ", np.median(heights))
print("75th percentile: ", np.percentile(heights, 75))

[165.22800319  87.82141828 109.19176656  20.23321914  55.52495932
  72.59458709 151.60410263  43.82968894  84.53099625 172.47296248
  90.90989587 107.25654201  21.11001655 144.60964009 105.53552247
  95.38690113  59.98367091  53.22113808  72.97888693 119.22763401
 153.20494731  89.32390906 117.12991202 102.5388967  109.35811287]
Mean height:  96.19229319557513
Standard deviation: 40.570450297029936
Minimum height:  20.233219138876752
Maximum height:  172.47296248187337
25th percentile:  72.59458709188556
Median:  95.38690113163136
75th percentile:  117.12991201839765

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn; seaborn.set()

plt.hist(heights)
plt.title('Height Distribution of US Presidents')
plt.xlabel('height (cm)')
plt.ylabel('number');

png

广播

广播允许这些二进制操作用于不同大小的数组

1 2	a = np.array([1, 2, 3]) a + 5

array([6, 7, 8])

可以认为这个操作是将数值5扩展或重复至数组[5, 5, 5]，然后执行加法
下面这个例子，一维数组为扩展或广播了，它沿着第二个维度扩展，扩展到匹配M数组的形状

1 2	M = np.ones((3, 3)) M + a

array([[2., 3., 4.],
       [2., 3., 4.],
       [2., 3., 4.]])

对两个数组同时广播，将 a 和b 都进行了扩展来匹配一个公共的形状，最终的结果是一个二维数组,例子如下：

a = np.arange(3)
b = np.arange(3)[:, np.newaxis]
print(a)
print(b)
a + b

[0 1 2]
[[0]
 [1]
 [2]]





array([[0, 1, 2],
       [1, 2, 3],
       [2, 3, 4]])

广播的规则

如果两个数组的维度数不相同，那么小维度数组的形状将会在最左边补 1
如果两个数组的形状在任何一个维度上都不匹配，那么数组的形状会沿着维度为 1 的维度扩展以匹配另外一个数组的形状
如果两个数组的形状在任何一个维度上都不匹配并且没有任何一个维度等于 1，那么会引发异常

示例1

一个二维数组与一个一维数组相加：

M = np.ones((2, 3))
a = np.arange(3)
形状如下

M.shape = (2, 3)
a.shape = (3,)
可以看到，根据规则1，数组a的维度数更小，所以在其左边补1

M.shape -> (2, 3)
a.shape -> (1, 3)
根据规则2，第一个维度不匹配，因此扩展这个维度以匹配数组

M.shape -> (2, 3)
a.shape -> (2, 3)
现在两个数组的形状匹配了，可以看到它们的最终形状都为(2, 3)

1
2
3

M = np.ones((2, 3))
a = np.arange(3)
M + a

array([[1., 2., 3.],
       [1., 2., 3.]])

示例2

两个数组都需要广播：

M = np.arange(3).reshape((3, 1))
a = np.arange(3)
形状如下

M.shape = (3,1)
a.shape = (3,)
可以看到，根据规则1，数组a的维度数更小，所以在其左边补1

M.shape -> (3, 1)
a.shape -> (1, 3)
根据规则2，需要更新这两个数组的维度来相互匹配

M.shape -> (3, 3)
a.shape -> (3, 3)
现在两个数组的形状匹配了，可以看到它们的最终形状都为(3, 3)

1
2
3

M = np.arange(3).reshape((3, 1))  
a = np.arange(3) 
M + a

array([[0, 1, 2],
       [1, 2, 3],
       [2, 3, 4]])

示例3

两个数组不兼容：

M = np.ones((3, 2))
a = np.arange(3)
形状如下

M.shape = (3, 2)
a.shape = (3,)
可以看到，根据规则1，数组a的维度数更小，所以在其左边补1

M.shape -> (3, 2)
a.shape -> (1, 3)
根据规则2，第一个维度不匹配，因此扩展这个维度以匹配数组

M.shape -> (3, 2)
a.shape -> (3, 3)
现在需要用到规则 3——最终的形状还是不匹配，因此这两个数组是不兼容的

1
2
3

M = np.ones((3,2))
a = np.arange(3) 
M + a

---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

<ipython-input-64-932af115d5e2> in <module>
      1 M = np.ones((3,2))
      2 a = np.arange(3)
----> 3 M + a


ValueError: operands could not be broadcast together with shapes (3,2) (3,)

广播的应用

数据的归一化

假设有一个有10个观察值的数组，每个观察值包含3个数值

X = np.random.random((10, 3))
计算每个特征的均值

Xmean = X.mean(0)
归一化操作

X_centered = X - Xmean

画一个二维数组

广播另外一个非常有用的地方在于，它能基于二维函数显示图像。我们希望定义一个函数 z = f (x, y)，可以用广播沿着数值区间计算该函数

x = np.linspace(0, 5, 50)
y = np.linspace(0, 5, 50)[:, np.newaxis]
z = np.sin(x) ** 10 + np.cos(10 + y * x) * np.cos(x)

x = np.linspace(0, 5, 50)  
y = np.linspace(0, 5, 50)[:, np.newaxis]  
z = np.sin(x) ** 10 + np.cos(10 + y * x) * np.cos(x)

plt.imshow(z, origin='lower', extent=[0, 5, 0, 5], cmap='viridis')
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x1409baa39b0>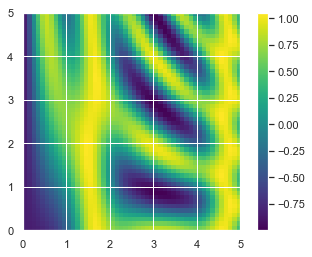

png

比较、掩码和布尔逻辑

比较操作

数组的逐元素操作,结果是一个布尔数据类型的数组

运算符	对应通用函数	描述
==	np.equal	等于
!=	np.not_equal	不等于
<	np.less	小于
<=	np.less_equal	小于等于
`>`	np.greater	大于
`>=`	np.greater_equal	大于等于

# 逐元素比较
x = np.array([1, 2, 3, 4, 5])
print(x < 3)
print(x > 3)
print(x <= 3)
print(x >= 3)
print(x != 3)
print(x == 3)
# 符合表达式实现两个数组的逐元素比较
print((2 * x) == (x ** 2))

[ True  True False False False]
[False False False  True  True]
[ True  True  True False False]
[False False  True  True  True]
[ True  True False  True  True]
[False False  True False False]
[False  True False False False]

操作布尔数组

统计记录的个数
np.count_nonzero(x < 6)
np.sum(x < 6) # False会被解释成0，True会被解释成1
- sum的好处是，可以沿着行或列进行
- 快速检车任意或所有的这些值是否为True
  np.any(x > 8)
  np.all(x < 0)
- 上述两个函数也可以通过指定axis来指定行列

rng = np.random.RandomState(0)
x = rng.randint(10, size=(3, 4))
print(np.count_nonzero(x < 6))
print(np.sum(x < 6))
print(np.any(x > 7))
print(np.all(x < 10))

8
8
True
True

布尔运算符

统计(0.5, 1)之间的数量和
np.sum((array > 0.5) & (inches < 1))
np.sum(~( (array <= 0.5) | (array >= 1) ))

运算符	通用函数
&	np.bitwise_and

^	np.bitwise_xor
~	np.bitwise_not

将布尔数组作为掩码

为了将特定值从数组中选出，可以进行简单的索引，即掩码操作

x[x < 5]
返回的是一个一维数组，它包含了所有满足条件的值。换句话说，所有的这些值是掩码数组对应位置为 True 的值。

# 例子
inches = np.random.random(365)*10
rainy = (inches > 3)
# 构建一个包含整个夏季日期的掩码（6月21日是第172天）
summer = (np.arange(365) - 172 < 90) & (np.arange(365) - 172 > 0)
print("Median precip on rainy days in 2014 (inches): ",
np.median(inches[rainy]))
print("Median precip on summer days in 2014 (inches): ",
np.median(inches[summer]))
print("Maximum precip on summer days in 2014 (inches): ",
np.max(inches[summer]))
print("Median precip on non-summer rainy days (inches):",
np.median(inches[rainy & ~summer]))

Median precip on rainy days in 2014 (inches):  6.3526921480470175
Median precip on summer days in 2014 (inches):  4.619087615684484
Maximum precip on summer days in 2014 (inches):  9.930332610947918
Median precip on non-summer rainy days (inches): 6.533648713530407

and 和 or 判断整个对象是真或假，而 & 和 | 是指每个对象中的比特位
- 使用 and 或 or 时，就等于让 Python 将这个对象当作整个布尔实体，所有非零的整数都会被当作是 True
  
  bool(-1), bool(0)
  (True, False)
  bool(-1 and 0)
  Flase
  bool(-1 or 0)
  True
- 对整数使用 & 和 | 时，表达式操作的是元素的比特，将 and 或 or 应用于组成该数字的每个比特
  
  bin(42)
  ‘0b101010’
  bin(59)
  ‘0b111011’
  bin(42 & 59)
  ‘0b101010’
  bin(42 | 59)
  ‘0b111011’
NumPy 中有一个布尔数组时，该数组可以被当作是由比特字符组成的，其中 1 = True、0 = False。这样的数组可以用上面介绍的方式进行 & 和 | 的操作：

1
2
3

A = np.array([1, 0, 1, 0, 1, 0], dtype=bool)
B = np.array([1, 1, 1, 0, 1, 1], dtype=bool)
A | B

array([ True,  True,  True, False,  True,  True])

而用 or 来计算这两个数组时，Python 会计算整个数组对象的真或假，这会导致程序出错
同样，对给定数组进行逻辑运算时，你也应该使用 | 或 &，而不是 or 或 and

1 2	x = np.arange(10) (x > 4) & (x < 8)

array([False, False, False, False, False,  True,  True,  True, False,
       False])

花哨的索引

探索花哨的索引

概念，传递一个索引数组来一次性获得多个数组元素

rand = np.random.RandomState(30)
x = rand.randint(100, size = 10)
# 传递索引的列表或数组来获取结果
ind = [3, 7, 4]
x[ind]

array([45, 53, 12])

结果的形状与索引数组的形状一致，而不是与被索引的数组形状一致

1 2	ind = np.array([[3, 7], [4, 5]]) x[ind]

array([[45, 53],
       [12, 23]])

对于多个维度的索引，和标准索引一样，第一个索引指的是行，第二个索引指的是列

X = np.arange(12).reshape((3, 4))
row = np.array([0, 1, 2])
col = np.array([2, 1, 3])
X[row, col]

array([ 2,  5, 11])

索引值的配对遵循广播的规则

1	X[row[:, np.newaxis], col]

array([[ 2,  1,  3],
       [ 6,  5,  7],
       [10,  9, 11]])

组合索引

花哨索引与其他索引方案结合使用

花哨索引和简单的索引组合使用

1	X[2, [2, 0, 1]]

array([10,  8,  9])

花哨索引和切片组合

1	X[1:, [2, 0, 1]]

array([[ 6,  4,  5],
       [10,  8,  9]])

花哨索引和掩码组合使用

1 2	mask = np.array([1, 0, 1, 0], dtype=bool) X[row[:, np.newaxis], mask]

array([[ 0,  2],
       [ 4,  6],
       [ 8, 10]])

示例：选择随机点

有一个 N×D 的矩阵，表示在 D 个维度的 N 个点
利用花哨的索引随机选取 20 个点——选择 20 个随机的、不重复的索引值，并利用这些索引值选取到原始数组对应的值
通常用于快速分割数据，即需要分割训练 / 测试数据集以验证统计模型时，以及在解答统计问题时的抽样方法中使用

# 构建数组
mean = [0, 0]
cov = [[1, 2],
      [2, 5]]
X = rand.multivariate_normal(mean, cov, 100)
X.shape

(100, 2)

1 2	# 绘画 plt.scatter(X[:, 0], X[:, 1]);

png

#选取随机点
indices = np.random.choice(X.shape[0], 20, replace=False)
selection = X[indices]
selection.shape

(20, 2)

# 画图
plt.scatter(X[:, 0], X[:, 1], alpha=0.3)
plt.scatter(selection[:, 0], selection[:, 1],
            facecolor='none', edgecolor='b', s=200);

png

用花哨索引修改值

x = np.arange(10)
i = np.array([2, 1, 8, 4])
x[i] = 99
print(x)

[ 0 99 99  3 99  5  6  7 99  9]

1 2	x[i] -= 10 print(x)

[ 0 89 89  3 89  5  6  7 89  9]

# 不会累加
x = np.zeros(10)
i = [2, 3, 3, 4, 4, 4]
x[i] += 1
x

array([0., 0., 1., 1., 1., 0., 0., 0., 0., 0.])

# 累加
x = np.zeros(10)
np.add.at(x, i, 1)
x

array([0., 0., 1., 2., 3., 0., 0., 0., 0., 0.])

示例：数据区间划分

创建一个数组

1
2
3

np.random.seed(42)
x = np.random.randn(100)
print(x)

[ 0.49671415 -0.1382643   0.64768854  1.52302986 -0.23415337 -0.23413696
  1.57921282  0.76743473 -0.46947439  0.54256004 -0.46341769 -0.46572975
  0.24196227 -1.91328024 -1.72491783 -0.56228753 -1.01283112  0.31424733
 -0.90802408 -1.4123037   1.46564877 -0.2257763   0.0675282  -1.42474819
 -0.54438272  0.11092259 -1.15099358  0.37569802 -0.60063869 -0.29169375
 -0.60170661  1.85227818 -0.01349722 -1.05771093  0.82254491 -1.22084365
  0.2088636  -1.95967012 -1.32818605  0.19686124  0.73846658  0.17136828
 -0.11564828 -0.3011037  -1.47852199 -0.71984421 -0.46063877  1.05712223
  0.34361829 -1.76304016  0.32408397 -0.38508228 -0.676922    0.61167629
  1.03099952  0.93128012 -0.83921752 -0.30921238  0.33126343  0.97554513
 -0.47917424 -0.18565898 -1.10633497 -1.19620662  0.81252582  1.35624003
 -0.07201012  1.0035329   0.36163603 -0.64511975  0.36139561  1.53803657
 -0.03582604  1.56464366 -2.6197451   0.8219025   0.08704707 -0.29900735
  0.09176078 -1.98756891 -0.21967189  0.35711257  1.47789404 -0.51827022
 -0.8084936  -0.50175704  0.91540212  0.32875111 -0.5297602   0.51326743
  0.09707755  0.96864499 -0.70205309 -0.32766215 -0.39210815 -1.46351495
  0.29612028  0.26105527  0.00511346 -0.23458713]

手动计算直方图

bins = np.linspace(-5, 5, 20)
counts = np.zeros_like(bins)
print(bins)
print(counts)

[-5.         -4.47368421 -3.94736842 -3.42105263 -2.89473684 -2.36842105
 -1.84210526 -1.31578947 -0.78947368 -0.26315789  0.26315789  0.78947368
  1.31578947  1.84210526  2.36842105  2.89473684  3.42105263  3.94736842
  4.47368421  5.        ]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]

为每个x找到合适的区间

1 2	i = np.searchsorted(bins, x) print(i)

[11 10 11 13 10 10 13 11  9 11  9  9 10  6  7  9  8 11  8  7 13 10 10  7
  9 10  8 11  9  9  9 14 10  8 12  8 10  6  7 10 11 10 10  9  7  9  9 12
 11  7 11  9  9 11 12 12  8  9 11 12  9 10  8  8 12 13 10 12 11  9 11 13
 10 13  5 12 10  9 10  6 10 11 13  9  8  9 12 11  9 11 10 12  9  9  9  7
 11 10 10 10]

为每个区间加上1

1	np.add.at(counts, i, 1)

计数数组 counts 反映的是在每个区间中的点的个数，即直方图分布
画出结果

1	plt.plot(bins, counts, linestyle='steps')

[<matplotlib.lines.Line2D at 0x1409bbe1710>]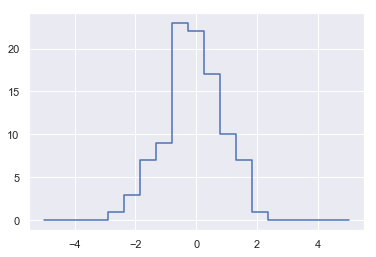

png

1 2	# 上述结果的另一种实现方法 plt.hist(x, bins, histtype='step');

png

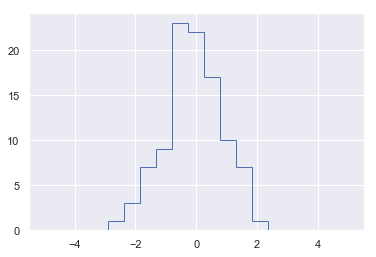
数组的排序

快速排序

np.sort

不修改原始输入数组的基础上返回一个排好序的数组
sort方法

用排序号的数组替代原始数组
np.argsort

返回原始数据排好序的索引值

1 2	x = np.array([3, 5, 2, 7, 8, 1]) np.sort(x)

array([1, 2, 3, 5, 7, 8])

1 2	x.sort() print(x)

[1 2 3 5 7 8]

1 2	x = np.array([3, 5, 2, 7, 8, 1]) np.argsort(x)

array([5, 2, 0, 1, 3, 4], dtype=int64)

按行或列排序，使用axis参数

axis=0，按列排序
axis=1，按行排序

rand = np.random.RandomState(42)
X = rand.randint(0, 10, (4, 6))
print(X)
print(np.sort(X, axis=0))
print(np.sort(X, axis=1))

[[6 3 7 4 6 9]
 [2 6 7 4 3 7]
 [7 2 5 4 1 7]
 [5 1 4 0 9 5]]
[[2 1 4 0 1 5]
 [5 2 5 4 3 7]
 [6 3 7 4 6 7]
 [7 6 7 4 9 9]]
[[3 4 6 6 7 9]
 [2 3 4 6 7 7]
 [1 2 4 5 7 7]
 [0 1 4 5 5 9]]

部分排序：分隔

np.partition

输入数组和数字K
输出是一个新数组，左边是第K小的值，右边是任意排序的其他值。两个分隔的区域中，元素都是任意排序
np.argpartition

计算分隔的索引值

1 2	x = np.array([7, 3, 5, 9, 2, 1, 4, 8]) np.partition(x, 3)

array([3, 1, 2, 4, 7, 5, 8, 9])

1 2	# 沿着多维数组的任意轴分隔 np.partition(X, 2, axis=1)

array([[3, 4, 6, 7, 6, 9],
       [2, 3, 4, 7, 6, 7],
       [1, 2, 4, 5, 7, 7],
       [0, 1, 4, 5, 9, 5]])

示例：K个最近邻

利用 argsort 函数沿着多个轴快速找到集合中每个点的最近邻

1
2
3

# 在二维平面上创建一个有10个随机点的集合
X = rand.rand(10, 2)
plt.scatter(X[:, 0], X[:, 1], s=100)

<matplotlib.collections.PathCollection at 0x1409bc845c0>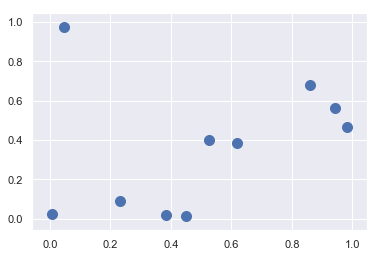

png

# 计算两两数据点对间的距离
dist_sq = np.sum((X[:,np.newaxis,:] - X[np.newaxis,:,:]) ** 2, axis=-1)
nearest = np.argsort(dist_sq, axis=1)
K = 2
nearest_partition = np.argpartition(dist_sq, K + 1, axis=1)
plt.scatter(X[:, 0], X[:, 1], s=100)
# 将每个点与它的两个最近邻连接
K = 2
for i in range(X.shape[0]):
    for j in nearest_partition[i, :K+1]:
        # 画一条从X[i]到X[j]的线段
        # 用zip方法实现：
        plt.plot(*zip(X[j], X[i]), color='black')

png

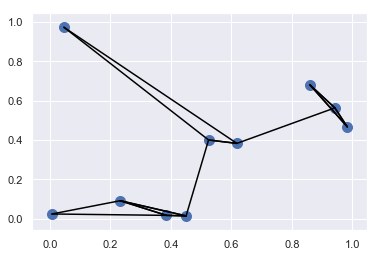
结构化数据

指定复合数据类型，构造一个结构化数组

x = np.zeros(4, dtype=int)
# 使用复合数据结构的结构化数组
data = np.zeros(4, dtype={'names':('name', 'age', 'weight'),
                         'formats':('U10', 'i4', 'f8')})
# U10表示‘长度不超过10的Unicode字符串’
# i4表示‘4字节（32比特）整型’
# f8表示‘8字节（64比特位）浮点型’
print(data.dtype)

[('name', '<U10'), ('age', '<i4'), ('weight', '<f8')]

name = ['Alice', 'Bob', 'Cathy', 'Doug']
age = [25, 45, 37, 19]
weight = [55.0, 85.5, 68.0, 61.5]
data['name'] = name
data['age'] = age
data['weight'] = weight
print(data)

[('Alice', 25, 55. ) ('Bob', 45, 85.5) ('Cathy', 37, 68. )
 ('Doug', 19, 61.5)]

1 2	# 获取所有名字 data['name']

array(['Alice', 'Bob', 'Cathy', 'Doug'], dtype='<U10')

1 2	# 获取数据第一行 data[0]

('Alice', 25, 55.)

1 2	# 获取最后一行的名字 data[-1]['name']

'Doug'

1 2	# 获取年龄小于30岁的人的名字 data[data['age'] < 30]['name']

array(['Alice', 'Doug'], dtype='<U10')

生成结构化数组

字典的方法

1 2	np.dtype({'names':('name', 'age', 'weight'), 'formats':('U10', 'i4', 'f8')})

dtype([('name', '<U10'), ('age', '<i4'), ('weight', '<f8')])

1
2
3

# 数值数据类型可以用 Python 类型或 NumPy 的 dtype 类型指定
np.dtype({'names':('name', 'age', 'weight'),
'formats':((np.str_, 10), int, np.float32)})

dtype([('name', '<U10'), ('age', '<i4'), ('weight', '<f4')])

1 2	# 元组列表 np.dtype([('name', 'S10'), ('age', 'i4'), ('weight', 'f8')])

dtype([('name', 'S10'), ('age', '<i4'), ('weight', '<f8')])

1 2	# 不指定类型的名称 np.dtype('S10,i4,f8')

dtype([('f0', 'S10'), ('f1', '<i4'), ('f2', '<f8')])

简写的字符串格式

第一个（可选）字符是 < 或者 >，分别表示“低字节序”（little endian）和“高字节序”（bid endian），表示字节（bytes）类型的数据在内存中存放顺序的习惯用法
后一个字符指定的是数据的类型：字符、字节、整型、浮点型，等等
最后一个字符表示该对象的字节大小

NumPy数据类型

NumPy数据类型符号	描述	示例
‘b’	字节型	np.dtype(‘b’)
‘i’	有符号整型	np.dtype(‘i4’) == np.int32
‘u’	无符号整型	np.dtype(‘u1’) == np.uint8
‘f’	浮点型	np.dtype(‘f8’) == np.int64
‘c’	复数浮点型	np.dtype(‘c16’) == np.complex128
‘S’、’a’	字符串	np.dtype(‘S5’)
‘U’	Unicode 编码字符串	np.dtype(‘U’) == np.str_
‘V’	原生数据，raw data（空，void）	np.dtype(‘V’) == np.void

跟高级的复合类型

创建一种类型，其中每个元素都包含一个数组或矩阵

tp = np.dtype([('id', 'i8'), ('mat', 'f8', (3, 3))])
X = np.zeros(1, dtype=tp)
print(X[0])
print(X['mat'][0])

(0, [[0., 0., 0.], [0., 0., 0.], [0., 0., 0.]])
[[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]

记录数组：结构化数组的扭转

np.recarray

域可以像属性一样获取，而不是像字典的键那样获取

1
2
3

# 消耗内存更多
data_rec = data.view(np.recarray)
data_rec.age

array([25, 45, 37, 19])

附：还有一些其他的

#读取数据
import numpy as np
nd10 = np.random.random([5,7])
np.savetxt(X=nd10,fname='test1.txt')
nd11 = np.loadtxt('test1.txt')
print(nd10,nd11)

[[0.417411   0.22210781 0.11986537 0.33761517 0.9429097  0.32320293
  0.51879062]
 [0.70301896 0.3636296  0.97178208 0.96244729 0.2517823  0.49724851
  0.30087831]
 [0.28484049 0.03688695 0.60956433 0.50267902 0.05147875 0.27864646
  0.90826589]
 [0.23956189 0.14489487 0.48945276 0.98565045 0.24205527 0.67213555
  0.76161962]
 [0.23763754 0.72821635 0.36778313 0.63230583 0.63352971 0.53577468
  0.09028977]] [[0.417411   0.22210781 0.11986537 0.33761517 0.9429097  0.32320293
  0.51879062]
 [0.70301896 0.3636296  0.97178208 0.96244729 0.2517823  0.49724851
  0.30087831]
 [0.28484049 0.03688695 0.60956433 0.50267902 0.05147875 0.27864646
  0.90826589]
 [0.23956189 0.14489487 0.48945276 0.98565045 0.24205527 0.67213555
  0.76161962]
 [0.23763754 0.72821635 0.36778313 0.63230583 0.63352971 0.53577468
  0.09028977]]

#截取数据
import numpy as np
np.random.seed(2019)
nd12 = np.random.random([10])
print(nd12)
print(nd12[3])
print(nd12[1:4])
print(nd12[2:9:2])
print(nd12[::-3])
nd13 = np.arange(25).reshape([5,5])
print(nd13)
print(nd13[1:2,1:4])
print(nd13[(nd13>4)&(nd13<9)])
print(nd13[[1,3]])
print(nd13[:,1:3])

[0.90348221 0.39308051 0.62396996 0.6378774  0.88049907 0.29917202
 0.70219827 0.90320616 0.88138193 0.4057498 ]
0.6378774010222266
[0.39308051 0.62396996 0.6378774 ]
[0.62396996 0.88049907 0.70219827 0.88138193]
[0.4057498  0.70219827 0.6378774  0.90348221]
[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]
 [15 16 17 18 19]
 [20 21 22 23 24]]
[[6 7 8]]
[5 6 7 8]
[[ 5  6  7  8  9]
 [15 16 17 18 19]]
[[ 1  2]
 [ 6  7]
 [11 12]
 [16 17]
 [21 22]]

#random.choice随机抽取
import numpy as np
from numpy import random as nr
a = np.arange(1,25,dtype=float)
c1 = nr.choice(a,size=(3,4))
c2 = nr.choice(a,size=(3,4),replace=False) #replace缺省为True，即可重复抽取
c3 = nr.choice(a,size=(3,4),p = a/np.sum(a))
print(c1)
print(c2)
print(c3)

[[19.  6. 24. 22.]
 [21. 17. 16.  2.]
 [23. 15. 13. 11.]]
[[ 5. 14. 23. 15.]
 [ 8. 24.  6. 18.]
 [13. 10. 21. 11.]]
[[19. 21. 18. 11.]
 [10. 21. 23. 19.]
 [18. 19. 11. 20.]]

#矩阵操作
import numpy as np
nd15 = np.arange(9).reshape([3,3])

#转置
print(np.transpose(nd15))

#乘法
a = np.arange(12).reshape([3,4])
b = np.arange(8).reshape([4,2])
print(a.dot(b))

#矩阵的迹
print(a.trace())

#计算行列式
print(np.linalg.det(nd15))

#逆矩阵
c = np.random.random([3,3])
print(np.linalg.solve(c,np.eye(3)))

[[0 3 6]
 [1 4 7]
 [2 5 8]]
[[ 28  34]
 [ 76  98]
 [124 162]]
15
0.0
[[ 0.79111977  4.79625456 -2.59458683]
 [ 0.72853989 -3.64821752  1.90992826]
 [-2.01814852 -5.08596471  4.61137684]]

#数据的合并与展平
import numpy as np
a = np.array([1,2,3])
b = np.array([4,5,6])
c = np.array([7,8,9])
print(np.append(a,b))
print(np.concatenate([a,b]))

[1 2 3 4 5 6]
[1 2 3 4 5 6]

#多维数组的合并
import numpy as np
a = np.arange(4).reshape(2,2)
b = np.arange(4).reshape(2,2)
#按行合并
print(np.append(a,b,axis=0))
#按列合并
print(np.append(a,b,axis=1))

[[0 1]
 [2 3]
 [0 1]
 [2 3]]
[[0 1 0 1]
 [2 3 2 3]]

#展平
import numpy as np
nd16 = np.arange(6).reshape(2,-1)
print(nd16)
#按列展平
print(nd16.ravel('F'))
#按行展平
print(nd16.ravel())

[[0 1 2]
 [3 4 5]]
[0 3 1 4 2 5]
[0 1 2 3 4 5]

列表与array的区别

导入numpy

array的创建

从列表创建数组

从头创建数组

Numpy数据类型

指定方式

数据类型

查看属性

数据的索引

获取单个元素

数据的切片

一维数组

多维子数组

行、列获取

非副本视图的子数组

创建数组的副本

数据的变形

数组的拼接和分裂

数组的拼接

数组的分裂

通用函数

数组的运算

绝对值

三角函数

指数和对数

高级的通用函数特性

指定输出

聚合

外积

聚合：最大值、最小值和其他值

1. 多维度聚合

2. 其他聚合函数

广播

广播的规则

示例1

示例2

示例3

广播的应用

数据的归一化

画一个二维数组

比较、掩码和布尔逻辑

比较操作

操作布尔数组

将布尔数组作为掩码

花哨的索引

探索花哨的索引

组合索引

示例：选择随机点

用花哨索引修改值

示例：数据区间划分

数组的排序

快速排序

部分排序：分隔

示例：K个最近邻

结构化数据

生成结构化数组

跟高级的复合类型

记录数组：结构化数组的扭转

附：还有一些其他的